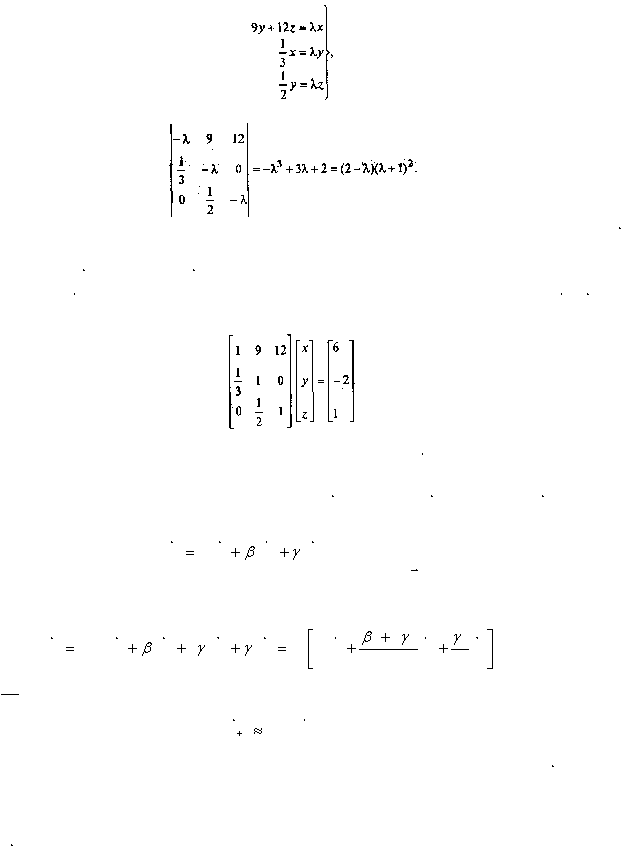
98
определитель которой
Следовательно, главное собственное число
?
1
= 2 и собственный вектор в силу (9.23) имеет вид
1
v
=
(24, 4,1). Остальные собственные числа в силу (9.24) имеют вид
?
2
=-1, ?3 =-1. В силу (9.23)
собственный вектор
2
v
имеет вид
2
v
= (6,-2,1). Так как собственное число -1 двукратно, то для
нахождения вектора
3
v
(называемого присоединенным), решаем систему уравнений (A- ?2)
3
v
=
2
v
:
Нетрудно проверить, что система (9.25) допускает решение
3
v
= (0, - 2, 2). Привлекая
геометрические соображения, заключаем, что возрастная структура популяции представляется
вектором в трехмерном пространстве, в котором векторы
1
v
= (24,4, 2),
2
v
= (6, - 2,1) и
v
= (0, - 2, 2) –
базисные, т. е.
,
3
0
2
0
1
0
0
v
v
v
a
a
(9.26)
где
?
0
, ?
0
, ?
0
– некоторые положительные числа (например, если
0
a
= (258, 30, 17), то
?
0
=10, ?
0
=3,
?
0
=2).
Тогда уравнение (9.21) примет вид:
.
2
2
2
2
3
0
2
0
0
1
0
3
0
2
0
2
0
1
0
v
v
k
v
a
v
v
k
v
v
a
a
k
k
k
k
k
(9.27)
Так как
k
k
2
> 0, k
> ?,
то при
t=+k > ? популяция возрастает по экспоненциальному закону
.
2
1
0
v
a
a
k
k
(9.28)
Главное собственное число
?
1
дает скорость, с которой возрастает размер популяции (в нашем
примере за каждый временной интервал популяция удваивается), а собственный вектор
1
v
определяет
устойчивую возрастную структуру популяции, т. е. отношение численностей особей разных возрастных
групп остается постоянным и равным 24:4:1. Нетрудно видеть, что если мы в конце каждого временного
интервала будем изымать половину популяции и использовать на корм, то размер ее станет равным
исходному
0
a
.
Матричные модели очень удобны для расчета на ЭВМ и находят все более широкое применение,
например, для анализа круговорота питательных веществ в экосистемах, в различных стохастических
моделях [54] (в марковских моделях и т.д.).
Контрольные задания
1. Показать, что график логистического уравнения имеет единственную точку перегиба. Найти ее и
дать биологическую интерпретацию.
(9.25)

