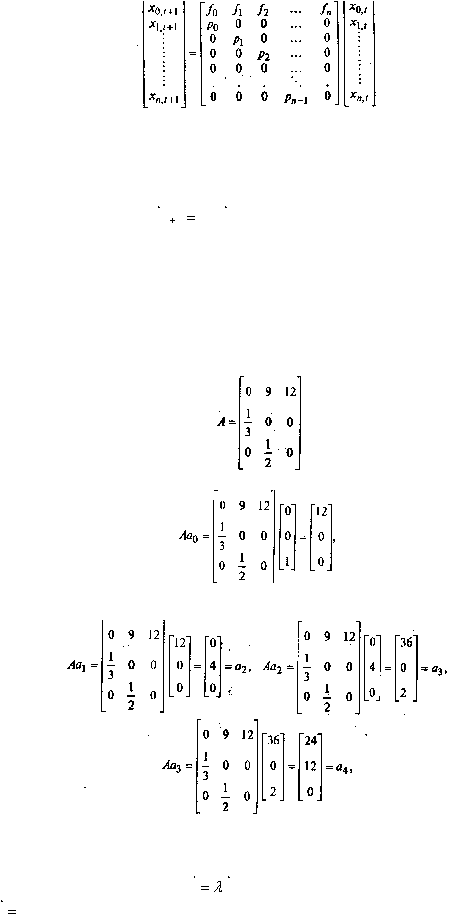
97
которое запишем в развернутом виде:
где величины f
i
,(i=0,1,...,n) представляют число самок, производимых самкой i-го возраста,
р, (i = 0,1,..., п -1) – вероятность того, что самка i-го возраста доживет до возраста i+1.
Покажем, что поведение модели можно предсказать, анализируя некоторые формальные свойства
матрицы А. Во-первых, последовательно умножая уравнение (9.19) на матрицу А, легко получить более
общие уравнения для численности возрастных групп к моменту времени
,
0
0
t
k
k
t
a
A
a
(9.21)
Во-вторых, поскольку матрица А квадратная с (n+1) строками и столбцами, она имеет n+1
собственных чисел (с учетом кратности) и (n+1) собственных (и присоединенных) векторов. Элементы
А являются либо положительными числами, либо нулями, поэтому наибольшее (по абсолютной
величине) собственное число и координаты отвечающего ему собственного вектора положительны и
при этом имеют определенный экологический смысл. Проиллюстрируем это на одной из простейших
моделей, предложенных Уильямсоном [54].
Исходная популяция имеет вектор, представляющий возрастную структуру а
0
= (0,0,1), т. е.
популяция состоит из одной самки старшего возраста. Матрица А имеет вид:
По прошествии одного временного интервала имеем
т. е. a1
= (12, 0, 0) и в популяции уже будет 12 самок младшего возраста. Повторное применение
модели дает следующие результаты:
и т.д.
Главное собственное число и собственный вектор матрицы А можно найти известными методами,
имея
v
v
A
(9.22)
или полагая
)
,
,
(
z
y
x
v
– систему линейных алгебраических уравнений

