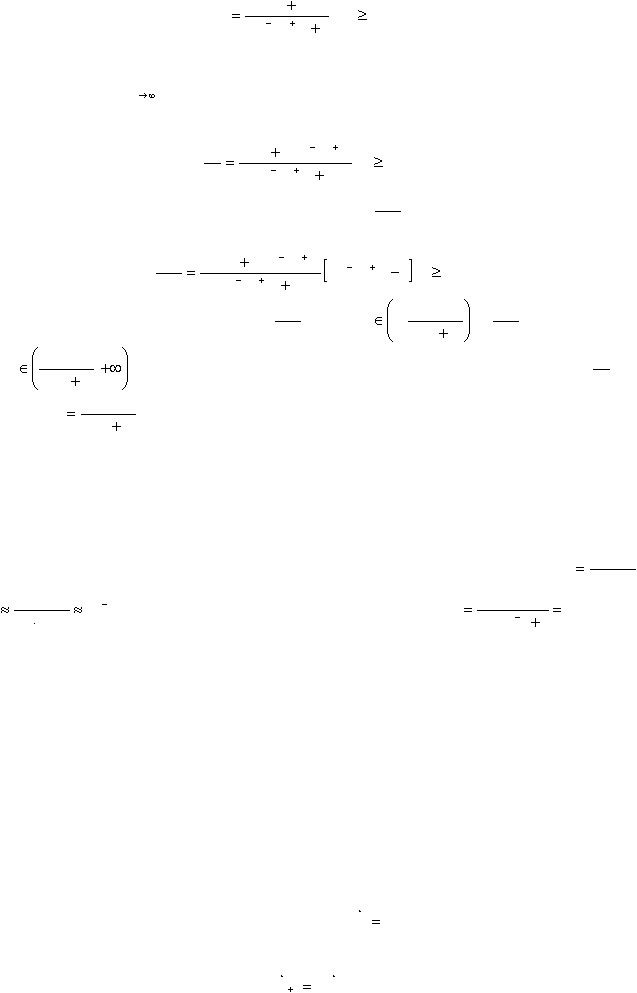
96
1
1
)
(t
)t
1
(
N
a
Ne
N
x
, t
0.
(9.16)
Итак, число заболевших – функция времени. Проанализируем эту функцию. Из уравнения (9.16)
вытекает, что с течением времени число заболевших может только увеличиваться, а все здоровые люди
заболеют, так как
)
(t
lim
x
t
=N+1. Конечно, это грубая модель, не учитывающая естественного
иммунитета у здоровых людей к данному заболеванию.
Интересно выяснить, как меняется скорость увеличения числа больных, т. е. величина
2
)t
1
(N
)t
1
(
2
)
1
(
)
1
(N
a
N
a
Ne
e
a
dt
dx
, t
0
(9.17)
Для решения этого вопроса нужно изучить величину
2
2
dt
x
d
.
Дифференцируя уравнение (9.17), получаем
1
)3
1
(Ne
)
1
(N
)t
1
(N
)t
1
(
)t
1
(N
3
2
2
2
a
N
a
a
Ne
e
a
dt
x
d
, t
0.
(9.18)
Из этого уравнения вытекает, что при
2
2
dt
x
d
> 0 при t
)
1
(
ln
,
0
N
a
N
и
2
2
dt
x
d
< 0 при
t
,
)
1
(
ln
N
a
N
. Следовательно, скорость возрастания заболевших – функция
dt
dx
– растет до
момента t
)
1
(
ln
N
a
N
, а затем убывает. Несмотря на грубость модели, этот результат совпадает с
экспериментальными данными: в начале эпидемии число заболевших резко возрастает, а впоследствии
скорость распространения инфекции снижается.
Для сравнения приведем результаты использования более сложных моделей развития гриппозной
эпидемии в Москве [22], где население составляет 8,5 млн человек. Это позволит нам также определить
численные значения параметров N и
?,
при которых наша модель более реалистична.
Началу эпидемии соответствует число заболевших 79,1 тыс. человек, откуда N = 8,5 млн./79,1 тыс.
?1100
человек. Пик заболеваемости приходится на 46
-й день, т. е. 46
1101
1100
ln
a
, откуда
4
10
1101
46
7
a
. По формуле (9.16) находим число больных
125
1
1101e
1101
)
46
(
5
x
. По отношению
к 1100 чел. это составляет 11%, что согласуется с экспериментальными данными [22], где число
больных равно 981 тыс. человек и составляет 11,5%. Конечно, применение соответствующих
профилактических мер дает значительный положительный эффект, пик числа больных снижается с
981тыс. до 122 тыс. человек, однако создание соответствующей математической модели – существенно
более трудная задача.
9.4. Матричные модели
Матричную модель можно рассматривать как конечно-разностный аналог динамической модели.
Один из ранних вариантов матричной модели был разработан Льюисом и Лесли [30] как
детерминистская модель, предсказывающая будущую возрастную структуру популяции самок по
известной структуре в настоящий момент времени и гипотетическим коэффициентам выживания и
плодовитости. Популяцию разбивают на n+1 возрастную группу (т. е. 0, 1, 2,..., п, причем каждая группа
состоит из особей одного возраста), так что самая старшая группа, или группа, в которой все
доживающие до данного возраста животные вымирают, имеет номер п. Обозначая через x
n
число особей
в каждой возрастной группе, получаем вектор
),
,...,
,
(x
1t
0t
nt
t
x
x
a
представляющий возрастную
структуру в момент времени t.
Модель описывается матричным уравнением
,
1
t
t
a
A
a
(9.19)

