95
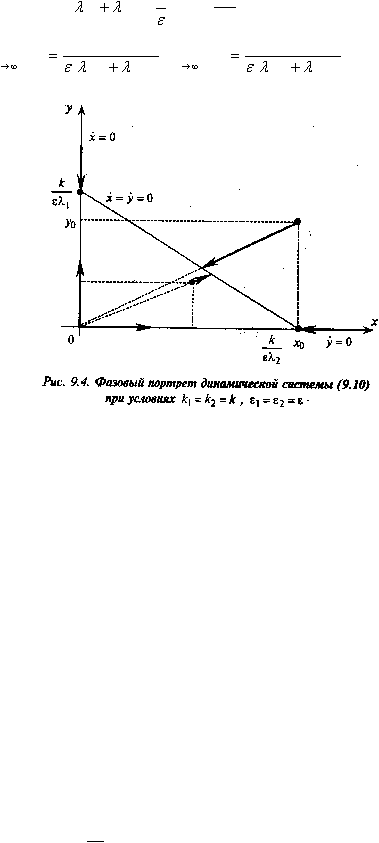
т. е. траекториями являются отрезки прямых, выходящих из начала координат (рис. 9.4). Обе
популяции не вымирают и численность их стабилизируется к значениям, которые можно найти как
координаты пересечения прямых
y
x
2
1
=
k
и y =
x
x
y
0
0
, откуда
,
)
(
)
(t
lim
0
2
0
1
0
y
x
kx
x
t
,
)
(
)
(t
lim
0
2
0
1
0
y
x
ky
y
t
(9.13)
9.3. Простейшая модель эпидемии
За многие годы существования человечества огромное число людей погибло от разных эпидемий.
Для того чтобы уметь бороться с эпидемиями, т. е. своевременно проводить тот или иной комплекс
мероприятий (прививки, вакцины, карантин и т.д.), необходимо уметь оценить эффективность каждого
такого комплекса и выбрать наиболее оптимальный для данного вида эпидемии (холера, чума, грипп,
СПИД и т.д.). Оценка эффективности базируется, как правило, на прогнозе о протекании эпидемии.
Отсюда вытекает задача построения модели, которая могла бы служить целям прогноза. Самой простой
моделью является описание естественного хода эпидемии без применения каких-либо
профилактических мероприятий.
Итак, пусть имеется N здоровых людей, и в момент времени t = 0 в эту группу попадает один
заболевший человек (источник инфекции). Предположим, что удаления заболевших из группы не
происходит и человек становится источником инфекции сразу же, как заразился сам.
Обозначим через x(t) число источников инфекции в момент времени t, а через y(t) – число еще не
заболевших (часть из них, естественно, может заболеть с течением времени). Очевидно, что х(t) + y(t) =
N +1 в любой момент времени t, причем при t = 0 выполняется условие х(0) = 1. Рассмотрим интервал
времени t, t +
?
t, где
?
t достаточно мало. Естественно, что число больных
?
х, появившихся за этот
интервал, пропорционально
?
t(
?
x??t). Естественно также предположить, что это число
пропорционально числу контактов между больными и здоровыми, т.е. произведению x(t)y(t). Таким
образом,
?
x??x(t)y(t)dt, где ? – коэффициент пропорциональности. Устремляя
?
t к нулю из последнего
соотношения, получим дифференциальное уравнение
dt
dx
=?x(t)(N+1-x(t)), (9.14)
которое вместе с начальным условием
х(0)=1 (9.15)
определяет функцию x(t). Уравнение (9.14) по виду является логистическим, оно рассмотрено в
предыдущем параграфе. Поэтому сразу можно записать решение x(t) задачи Коши (9.14), (9.15) в
удобном виде

