94
х=0 и
y
x
2
1
=
1
1
k
,
а у=0 также на двух прямых:
у=0 и
y
x
2
1
=
2
2
k
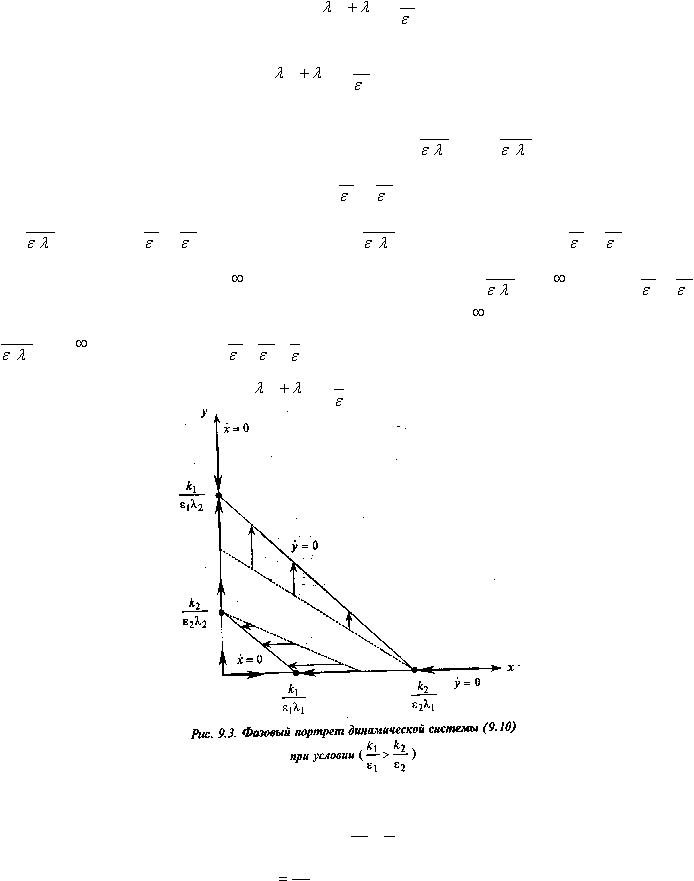
(рис. 9.2, 9.3).
По этим рисункам можно сделать следующие выводы. В обоих случаях имеем три стационарные
точки, в которых одновременно х=0 и у=0, а именно: (0,0), (0,
1
1
1
k
) и (0,
2
2
2
k
), которые по известной
классификации являются узлами. При этом, если
1
1
k
>
2
2
k
(рис. 9.2), то устойчивым является только
узел (
1
1
1
k
, 0), а если
1
1
k
<
2
2
k
(рис. 9.3), то узел (0,
2
2
2
k
). Таким образом, если
1
1
k
>
2
2
k
, то вторая
популяция вымирает, y(t)
> 0,
t
>
, а первая стабилизируется, x(t)
>
1
1
1
k
, t
>
. Если же
1
1
k
<
2
2
k
,
то имеем обратную картину: первая популяция вымирает, x(t)
>
0, t>
, а вторая стабилизируется, x(t)
>
2
2
2
k
, t>
. Наконец, если
1
1
k
=
2
2
k
=
k
, то кроме неустойчивого узла (0,0) имеем линию
стационарных точек – отрезок прямой
y
x
2
1
=
k
(рис. 9.3).
В дальнейших рассмотрениях будем для простоты считать, что k1=k2=k и ?1= ?2= ?.
Тогда, деля
второе уравнение системы (9.10) на первое, получим
dx
dy
=
x
y
, откуда
)
(t
)
(t
0
0
x
x
y
y
, (9.12)

