93
y
y)
x
x(
y
k2
dt
dy
x
y)
x
x(
x
k
dt
dx
2
1
1
2
1
1
1
, (9.10)
где
2
1
2
1
2
1
,
,
,
,
,
k
k
– определенные положительные числа.
Первые члены правых частей системы (9.10) характеризуют скорость роста популяций при
отсутствии ограничивающих факторов. Вторые члены учитывают те изменения в скоростях, которые
вызываются ограниченностью корма.
Задавая различные значения параметров, с помощью системы (9.10) можно описать взаимодействие
двух популяций, одна из которых – хищник, а другая – жертва [36]. В литературе [47] более подробно
описаны математические аспекты исследования системы (9.10).
Прежде чем исследовать, как будет вести себя система (9.10), заметим, что в любой момент времени t
ее состояние полностью описывается значениями х и у: каждому состоянию системы соответствует
некоторая точка (х, у) на плоскости хОу, называемой «фазовой плоскостью». Каждой точке фазовой
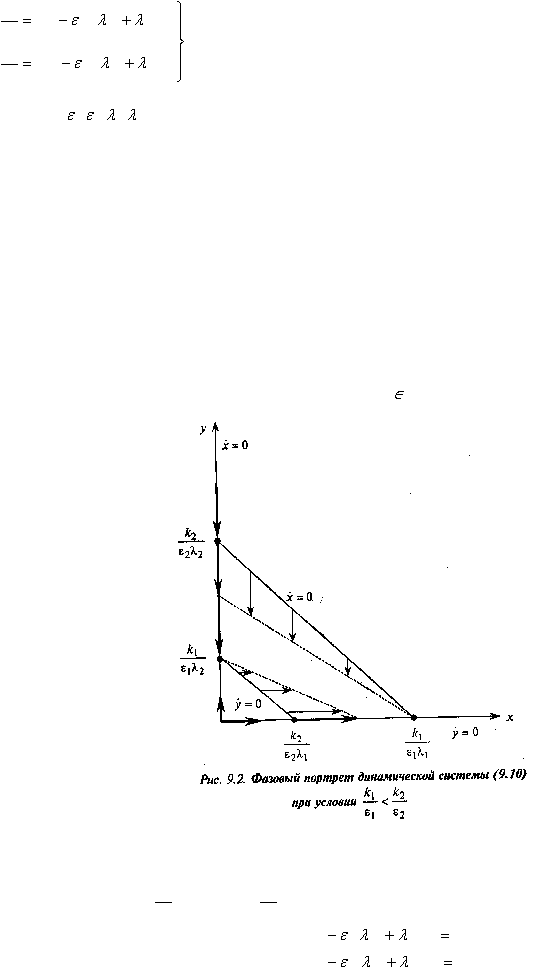
плоскости можно поставить в соответствие вектор (стрелку на рис. 9.2) с координатами, которые
являются правыми частями системы, указывающий направление движения в этой точке. Проведя из
начальной точки линии, касательные этим векторам, получим траектории, по которым будет
происходить движение системы, т. е. решения задачи Коши для системы (9.10) с начальными
условиями
x(t
0
)=x
0
, y(t
0
)=y
0
, (х
0
,у
0
)
х0у. (9.11)
Чтобы составить представление о траекториях движения системы, построим линии, на которых х=0
(здесь векторы параллельны оси Оу) и у = 0 (здесь векторы параллельны оси Ох). Для краткости
обозначим производную
dt
dx
– через х, а
dt
dy
– через у. Имеем
х=0, когда
0
)
(
2
1
1
1
x
y
x
x
k
,
у=0, когда
0
)
(
2
1
2
2
y
y
x
x
k
,
т. е. х = 0 на двух прямых в фазовой плоскости:

