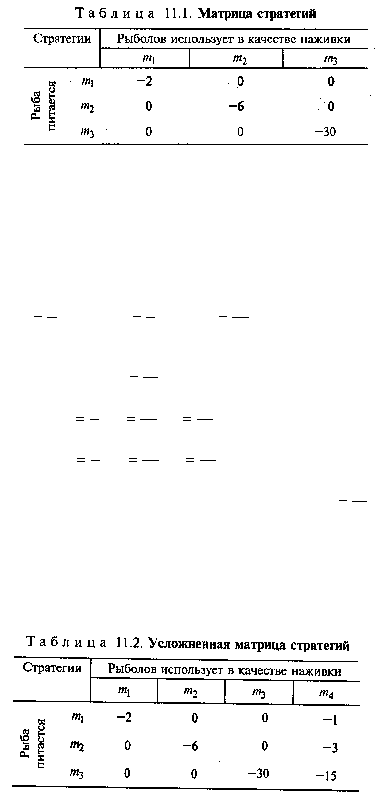
112
На основании изложенных утверждений достаточно найти неотрицательные числа х1,х2,х3, y1,y2,y3 и
число, удовлетворяющее следующим условиям:
x1+x2+x3=l, y1+y2+y3=1,
(11.27)
v
?
-2x1,
-2y1 ? v,
v
?
-6x2,
-6у2 ? v,
v
?
-30x3,
-30у3
?
v.
Заменим последние шесть неравенств на равенства. Тогда имеем
х1=у1=
2
v
, x2=y2=
6
v
, x3=у3=
30
v
.
(11.28)
Подставляя эти значения в равенства (11.27), получим
v =
7
10
.
(11.29)
21
1
,
21
5
,
7
5
3
2
1
x
x
x
.
(11.30)
21
1
,
21
5
,
7
5
3
2
1
y
y
y
(11.31)
Таким образом, цена игры для рыбы будет отрицательной и равной
7
10
. Она показывает, что в
конце концов рыба будет поймана. При этом оптимальная стратегия рыбака совпадает со стратегией
питания (также оптимальной) рыбы и оптимальная стратегия уменьшает вероятность поимки рыбы в
каждом конкретном случае.
Несколько усложним задачу. Предположим, что рыболов иногда использует приманку т
4
, которая
может быть принята по ошибке за одно из трех насекомых, но которая вдвое чаще вызывает подозрение
у рыб. Тогда матрица С стратегий ловли на удочку и питания рыб примет вид табл. 11.2:
Теперь достаточно найти неотрицательные числа х1,х2,х3, y1,y2,y3,y
4
и число v, удовлетворяющие
следующим условиям:
x1+x2+x3=l,
y1+y2+y3+y
4
=1,
(11.27)
v
?
-2x1,
-y
4
–2y1 ? v,
v
?
-6x2,
-3y
4
– 6у2 ? v,
v
?
-30x3,
-15y
4
–
30у3
?
v.
v
?
-x1 –3x2 –15 x3
Левая система неравенства переопределена, а правая недоопределена (в левой неизвестных больше,
чем неравенств, а в правой меньше). Заметим, что если последнее неравенство в правой колонке
-15y
4
–30у3
?
v. будет выполнено при у3=0, то оно будет выполнено и при всех у3>0. Следовательно,
полагая у3 = 0, правую систему неравенств можно заменить системой трех линейных уравнений

