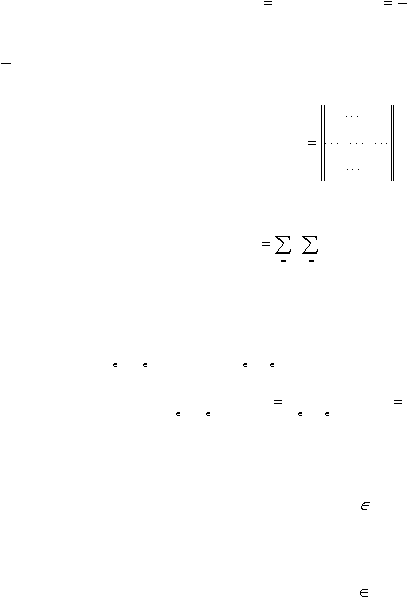
111
Отметим также, что в рассмотренном примере мы показали существование оптимальных стратегий и
установили равенство
5
4
)
,
(x
min
max
)
(
min
max
y
E
xy
E
x
y
y
x
;
(11.22)
при этом величину Е(х,у) можно трактовать как математическое ожидание выигрыша, а величину
v =
5
4
определить как цену игры.
Рассмотрим теперь общий случай прямоугольной матрицы
mn
m¹
n
c
c
c1
c
C
11
.
При любой допустимой стратегии игрока A: x1
? 0, ...,
х
m
? 0,
x1 +x2+…+x
m
=1 и любой допустимой
стратегии игрока В: y1
? 0, ...,
y
m
? 0,
y1 +y2+…+y
m
=1 математическое ожидание выигрыша равно
n
j
j
i
ij
m
i
y
x
c
y)
x,
E(
1
1
.
(11.23)
Множество допустимых стратегий x = (x1,…,x
n
)
игрока А обозначим через X, а множество
допустимых стратегий у=(у1,...,y
n
) игрока В обозначим через Y.
Рассмотренные выше примеры являются частными случаями общих теорем [18] для игр с
прямоугольными матрицами (прямоугольными играми); из них, в частности, вытекает:
1. Величины
)
,
(
min
max
)
,
(
min
max
y
x
E
и
y
x
E
X
x
Y
у
Y
y
X
x
существуют и равны между собой; при этом
величина
v
y)
x,
E(
y)
x,
E(
X
x
Y
у
Y
y
X
x
min
max
min
max
(11.24)
является ценой игры.
2. Всякая прямоугольная игра имеет цену; каждый игрок в прямоугольной игре всегда имеет
оптимальную стратегию.
3. Пусть Е – математическое ожидание выигрыша в прямоугольной игре с матрицей С, имеющей
цену v. Тогда для того, чтобы элемент х
*
=(х1
*
,...,х
*
m
)
Х был оптимальной стратегией для игрока А,
необходимо и достаточно, чтобы для всякого j =1, 2,...,n базисного вектора y
(j)
=
)
0
,...,
0
,
1
,
0
,...,
0
(
j
имело
место неравенство
v
? E (x
*
, y
(j)
).
(11.25),
Аналогично для того чтобы элемент у
*
=(y
*
1
,...,y
*
n
)
Y был оптимальной стратегией для игрока В,
необходимо и достаточно, чтобы для всякого элемента базисного вектора x
(i)
=
)
0
,...,
0
,
1
,
0
,...,
0
(
i
имело
место неравенство
E (x
(i)
, y
*
)
? v.
(11.26)
Покажем теперь на двух примерах, как можно применить эти утверждения для вычисления цен и
определения оптимальных стратегий для прямоугольных игр. В качестве таких примеров рассмотрим
стратегии ловли на удочку и питания рыбы¹.
1
Идея примера взята из книги Вильямса [8], которая также может служить хорошим введением в теорию игр.
Представим себе, что существование такого вида рыб, питающихся у поверхности воды, зависит от
наличия трех видов летающих насекомых, которые обозначим через т1,т2 и m3 соответственно;
насекомые появляются в зоне захвата с частотами 15п, 5п и п (т. е. насекомых т2 в 5 раз больше чем m3,
а насекомых т1 в 3 раза больше чем т2).
Допустим, что рыбак В ловит рыбу А на насекомых одного из этих видов, насаживая их на крючок.
Тогда матрица стратегий С ловли на удочку и питания рыб имеет следующий вид (табл. 11.1):

