7
d) т
A
> m
B
, S
A
> S
B
;
e) т
A
< m
B
, S
A
< S
B
.
В последних двух случаях решение о выборе проекта А или В зависит от отношения к риску ЛПР.
В частности, в случае d проект А обеспечивает более высокую среднюю прибыль, однако он и более
рискован. Выбор при этом определяется тем, какой дополнительной величиной средней прибыли
компенсируется для ЛПР заданное увеличение риска. В случае е для проекта А риск меньший, но и
ожидаемая прибыль меньшая. Субъективное отношение к риску учитывается в теории Неймана-
Моргенштерна и рассматривается в гл. 4.
Пример. Пусть имеются два инвестиционных проекта. Первый с вероятностью 0,6 обеспечивает
прибыль 15 млн руб., однако с вероятностью 0,4 можно потерять 5,5 млн руб. Для второго проекта с
вероятностью 0,8 можно получить прибыль 10 млн руб. и с вероятностью 0,2 потерять 6 млн руб.
Какой проект выбрать?
Решение. Оба проекта имеют одинаковую среднюю прибыльность, равную 6,8 млн руб. (0,6*15
+ +0,4(-5,5)=0,8*10 + 0,2(-6) = 6,8). Однако среднее квадратичное отклонение прибыли для первого
проекта равно 10,04 млн руб. ([0,6(15 - 6,8)² + 0,4(-5,5 – 6,8)²]¹
/2
= 10,04), а для второго - 6,4 млн руб.
([0,8 (10 - 6,8)² + 0,2(-6 – 6,8)²]
1/2
= 6,4), поэтому более предпочтителен второй проект.
Хотя среднее квадратичное отклонение эффективности решения и используется часто в качестве
меры риска, оно не совсем точно отражает реальность. Возможны ситуации, при которых варианты
обеспечивают приблизительно одинаковую среднюю прибыль и имеют одинаковые средние
квадратичные отклонения прибыли, однако не являются в равной мере рискованными.
Действительно, если под риском понимать риск разорения, то величина риска должна зависеть от
величины исходного капитала ЛПР или фирмы, которую он представляет. Теория Неймана-
Моргенштерна это обстоятельство учитывает. Из публикаций, посвященных методам измерения и
управления рисками, укажем на [8,9,10,16,18,20].
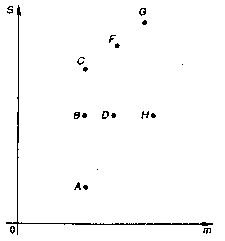
На рис. 1.1 рассмотрен случай выбора из более чем двух вариантов инвестиций. Характеристики
вариантов показаны точками на плоскости (т, S), где т - средняя прибыль, получаемая в результате
инвестиции, а S- среднее квадратичное отклонение прибыли.
Рис. 1.1. Варианты выбора инвестиций
Из рис. 1.1 видно, что среди вариантов А, В и С наиболее предпочтителен А. Из вариантов В, D и Н
следовало бы выбрать Н. Вариант Н лучше вариантов С и
F. Однако сравнительная
предпочтительность, например, вариантов А, D, F и G зависит от склонности ЛПР к риску.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Что такое риск?
2. Какие бывают виды рисков?
3. Какой параметр наиболее часто используется в качестве меры риска?
4. Акционерному обществу предлагаются два рисковых проекта:
Проект I
Проект 2
Вероятность события ................................. 0,2 0,6 0,2
0,4 0,2 0,4
Наличные поступления, млн руб. ........... 40 50 60
0 50 100
Учитывая, что фирма имеет фиксированные платежи по долгам 80 млн руб., какой проект должны
выбрать акционеры и почему?

