8
ГЛАВА 2 СТРАТЕГИЧЕСКИЕ ИГРЫ
2.1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ СТРАТЕГИЧЕСКИХ ИГР
На практике часто появляется необходимость согласования действии фирм, объединении,
министерств и других участников проектов в случаях, когда их интересы не совпадают. В таких
ситуациях теория игр позволяет найти лучшее решение для поведения участников, обязанных
согласовывать действия при столкновении интересов. Теория игр все шире проникает в практику
экономических решений и исследований. Ее можно рассматривать как инструмент, помогающий
повысить эффективность плановых и управленческих решений. Это имеет большое значение при
решении задач в промышленности, сельском хозяйстве, на транспорте, в торговле, особенно при
заключении договоров с иностранными государствами на любых иерархических уровнях. Так, можно
определить научно обоснованные уровни снижения розничных цен и оптимальный уровень товарных
запасов, решать задачи экскурсионного обслуживания и выбора новых линий городского транспорта,
задачу планирования порядка организации эксплуатации месторождений полезных ископаемых в
стране и др. Классической стала задача выбора участков земли под сельскохозяйственные культуры.
Метод теории игр можно применять при выборочных обследованиях конечных со-вокупностей, при
проверке статистических гипотез.
Обычно теорию игр определяют как раздел математики для изучения конфликтных ситуаций. Это
значит, что можно выработать оптимальные правила поведения каждой стороны, участвующей в
решении конфликтной ситуации.
В экономике, например, оказался недостаточным аппарат математического анализа,
занимающийся определением экстремумов функций. Появилась необходимость изучения так
называемых оптимальных минимаксных и максиминных решений. Следовательно, теорию игр
можно рассматривать как новый раздел оптимизационного подхода, позволяющего решать новые
задачи при принятии решений.
Игра - упрощенная формализованная модель реальной конфликтной ситуации. Математически
формализация означает, что выработаны определенные правила действия сторон в процессе игры:
варианты действия сторон; исход игры при данном варианте действия; объем информации каждой
стороны о поведении всех других сторон.
Одну играющую сторону при исследовании операций может представлять коллектив,
преследующий некоторую общую цель. Однако разные члены коллектива могут быть по-разному
информированы об обстановке проведения игры.
Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не
рассматриваются, хотя не всякий выигрыш в действительности можно оценивать количественно.
Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из
возможных ситуаций игры. Существуют игровые системы управления, если процесс управления в
них рассматривается как игра.
Платежная матрица (матрица эффективности, матрица игры) включает все значения выигрышей (в
конечной игре). Пусть игрок 1 имеет т стратегий А
i
, а игрок 2 -
п стратегий В
j
, (
m
i
,
1
;
n
j
,
1
).
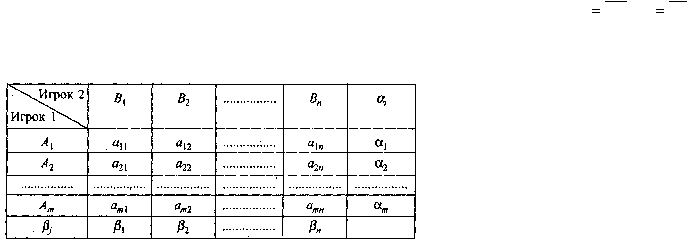
Игра может быть названа игрой тхп. Представим матрицу эффективности игры двух лиц с нулевой
суммой, сопроводив ее необходимыми обозначениями (табл. 2.1).
Таблица 2.1
В данной матрице элементы
ij
a
– значения выигрышей игрока 1 – могут означать и
математическое ожидание выигрыша (среднее значение), если выигрыш является случайной величи-

