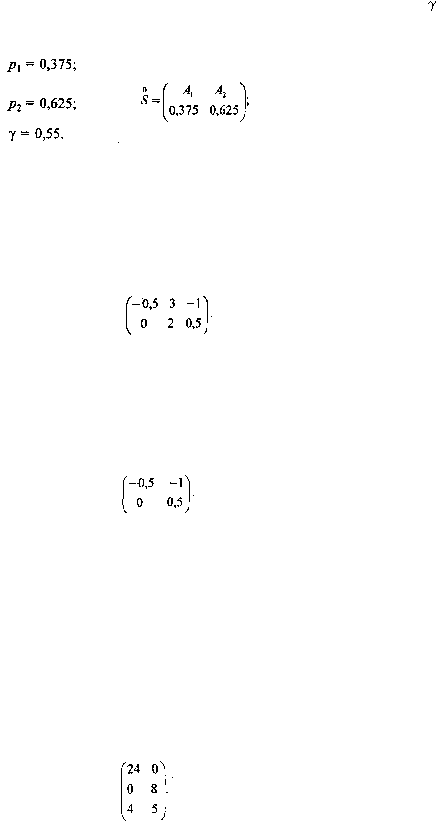
16
Алгоритм решения:
1. По оси абсцисс отложим отрезок единичной длины.
2. По оси ординат отложим выигрыши при стратегии А1.
3. На вертикали в точке 1 отложим выигрыши при стратегии А2.
4. Проводим прямую b
11
b
12
, соединяющую точки а
11
,a
21
.
5. Проводим прямую b
21
b
22
, соединяющую точки а
12
, а
22
.
6. Определяем ординату точки пересечения с линий b
11
b
12
и b
21
b
22
. Она равна
.
7. Определим абсциссу точки пересечения с. Она равна р2, а р1=1–р2
Выпишем решение и представим оптимальную стратегию игры:
Вывод. При установке новой системы ЭВМ, если неизвестны условия решения задач заказчика, на
работу ЭВМ А1 должно приходиться 37,5 % времени, а на работу ЭВМ А2
- 62,5 %. При этом
выигрыш составит 55 % по сравнению с предыдущей системой ЭВМ.
2.4. МАЖОРИРОВАНИЕ (ДОМИНИРОВАНИЕ) СТРАТЕГИЙ
Мажорирование представляет отношение между стратегиями, наличие которого во многих
практических случаях дает возможность сократить размеры исходной платежной матрицы игры.
Рассмотрим это понятие на примере матрицы
Рассуждая с позиции игрока 2, можно обнаружить преимущество его третьей стратегии перед
второй, поскольку при первой стратегии игрока 1 выигрыш игрока 2 равен —3 (вторая стратегия) и 1
(третья стратегия), а при второй стратегии игрока 1 выигрыш игрока 2 равен —2 (вторая стратегия) и
- 0,5 (третья стратегия). Таким образом, при любой стратегии игрока 1 игроку 2 выгоднее применять
свою третью стратегию по сравнению со второй; при наличии третьей стратегии игрок 2, если он
стремится играть оптимально, никогда не будет использовать свою вторую стратегию, поэтому ее
можно исключить из игры, т.е. в исходной платежной матрице можно вычеркнуть 2-й столбец:
С позиции игрока 1 его первая стратегия оказывается хуже второй, так как по первой стратегии он
только проигрывает. Поэтому первую стратегию можно исключить, а матрицу игры преобразовать к
виду:
(0 0,5).
Учитывая интересы игрока 2, следует оставить только его первую стратегию, поскольку, выбирая
вторую стратегию, игрок 2 оказывается в проигрыше (0,5 - выигрыш игрока 1), и матрица игры
принимает простейший вид: (0), т.е. имеется седловая точка.
Мажорирование можно распространить и на смешанные стратегии. Если элементы одной строки
не все меньше (или равны) соответствующих элементов других строк, но все меньше (или равны)
некоторых выпуклых линейных комбинаций соответствующих элементов других строк, то эту
стратегию можно исключить, заменив ее смешанной стратегией с соответствующими частотами
использования чистых стратегий.
В качестве иллюстрации к сказанному рассмотрим матрицу игры:
Для первых двух чистых стратегий игрока 1 возьмем частоты их применения (вероятности)
равными 0,25 и 0,75.
Третья стратегия игрока 1 мажорируется линейной выпуклой комбинацией первой и второй
чистых стратегий, взятых с частотами 0,25 и 0,75 соответственно, т.е. смешанной стратегией:

