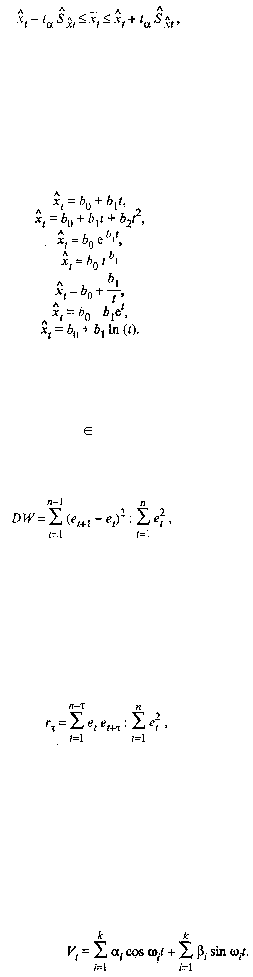
454
(54.3)
где t
?
— табличное значение, определяемое по t-распределению Стьюдента при уровне значимости
?
и
числе степеней свободы п - k.
В литературе представлено большое число математико-статистических моделей для адекватного
описания разнообразных тенденций временных рядов.
Наиболее распространенными видами трендовых моделей, характеризующих монотонное
возрастание или убывание исследуемого явления, являются:
(54.4)
Правильно выбранная модель должна соответствовать характеру изменений тенденции исследуемого
явления; При этом величина е
t
должна носить случайный характер с нулевой средней.
Кроме того, ошибки аппроксимации e
t
должны быть независимыми между собой и подчиняться
нормальному закону распределения e
t
N
(0, ?). Независимость ошибок e
t
, т.е. отсутствие
автокорреляции остатков, обычно проверяется по критерию Дарбина—Уотсона, основанного на
статистике:
(54.5)
где e
t
= x
t
-
t
x
ˆ
.
Если отклонения не коррелированы, то величина
DW приблизительно равна двум. При наличии
положительной автокорреляции 0
?
DW ? 2, а отрицательной — 2
?
D W ? 4.
О коррелированности остатков можно также судить по коррелограмме для отклонений от тренда,
которая представляет собой график функции относительно
?
коэффициента автокорреляции, который
вычисляется по формуле
(54.6)
где
? = 0, 1, 2 ... .
После выбора наиболее подходящей аналитической функции для тренда его используют для
прогнозирования на основе экстраполяции на заданное число временных интервалов.
Рассмотрим задачу сглаживания сезонных колебаний, исходя из ряда V
t
= х
t
-
t
x
ˆ
, где x
t
— значение
исходного временного ряда в момент t, а
t
x
ˆ
— оценка соответствующего значения тренда (t = 1, 2, ..., п).
Так как сезонные колебания представляют собой циклический, повторяющийся во времени процесс,
то в качестве сглаживающих функций используется гармонический ряд (ряд Фурье) следующего вида:
Оценки параметров
?
i
и
?
i
модели определяют из выражений

