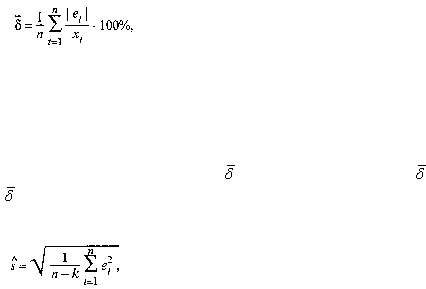
453
4.
В чем состоит задача компонентного анализа, как интерпретировать главные компоненты и определить
их вклад в суммарную дисперсию?
5.
Какие задачи решает кластерный анализ? В чем особенности иерархических кластер-процедур?
Глава 54. Экономико-математические методы прогнозирования социально-
экономических процессов
54.1. Трендовые модели прогнозирования
Статистические наблюдения в социально-экономических исследованиях обычно проводятся
регулярно через равные отрезки времени и представляются в виде временных рядов x
t
, где t = 1, 2, ..., п.
В качестве инструмента статистического прогнозирования временных рядов служат трендовые
регрессионные модели, параметры которых оцениваются по имеющейся статистической базе, а затем
основные тенденции (тренды) экстраполируются на заданный интервал времени.
Методология статистического прогнозирования предполагает построение и испытание многих
моделей для каждого временного ряда,
их
сравнение на основе статистических критериев и отбор
наилучших из них для прогнозирования.
При моделировании сезонных явлений в статистических исследованиях различают два типа
колебаний: мультипликативные и аддитивные. В мультипликативном случае размах сезонных
колебаний изменяется во времени пропорционально уровню тренда и отражается в статистической
модели множителем. При аддитивной сезонности предполагается, что амплитуда сезонных отклонений
постоянна и не зависит от уровня тренда, а сами колебания представлены в модели слагаемым.
Основой большинства методов прогнозирования является экстраполяция, связанная с
распространением закономерностей, связей и соотношений, действующих в изучаемом периоде, за его
пределы, или — в более широком смысле слова — это получение представлений о будущем на основе
информации, относящейся к прошлому и настоящему.
Наиболее известны и широко применяются трендовые и адаптивные методы прогнозирования. Среди
последних можно выделить такие, как методы авторегрессии, скользящего среднего (Бокса —
Дженкинса и адаптивной фильтрации), методы экспоненциального сглаживания (Хольта, Брауна и
экспоненциальной средней) и др.
Для оценки качества исследуемой модели прогноза используют несколько статистических критериев.
Наиболее распространенными критериями являются следующие.
Относительная ошибка аппроксимации:
(54.1)
где e
t
= х
t
-
t
x
ˆ
— ошибка прогноза;
х
t
— фактическое значение показателя;
t
x
ˆ
— прогнозируемое значение.
Данный показатель используется в случае сравнения точности прогнозов по нескольким моделям.
При этом считают, что точность модели является высокой, когда
< 10%, хорошей — при
= 10—
20% и удовлетворительной — при
= 20—50%.
Средняя квадратическая ошибка:
(54.2)
где k — число оцениваемых коэффициентов уравнения.
Наряду с точечным в практике прогнозирования широко используют интервальный прогноз. При
этом доверительный интервал чаще всего задается неравенствами

