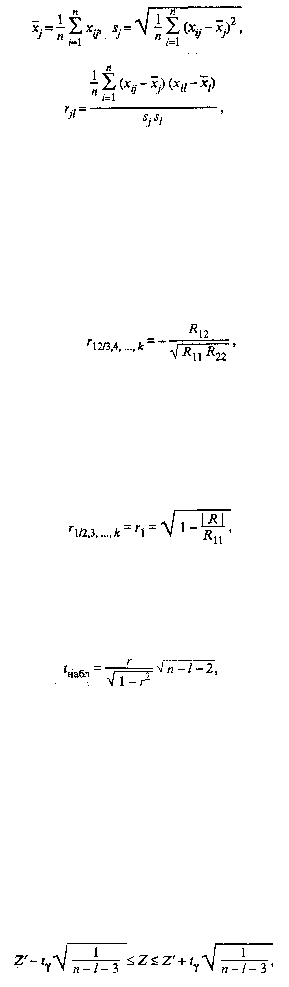
427
где
(53.1)
(53.2)
x
ij
— значение i-го наблюдения j-го фактора,
r
il
— выборочный парный коэффициент корреляции, характеризующий тесноту линейной связи
между показателями x
j
и x
l
. При этом r
jl
является оценкой генерального парного коэффициента
корреляции.
Матрица R является симметричной (r
jl
= r
lj
) и положительно определенной.
Кроме того, находятся точечные оценки частных и множественных коэффициентов корреляции
любого порядка. Например, частный коэффициент корреляции (k - 2)-го порядка между переменными х1
и х2 равен
(53.3)
где
R
jl
— алгебраическое дополнение элемента r
jl
корреляционной матрицы R. При этом R
jl
= (-l)
j+l
M
jl
,
где M
jl
— минор, т.е. определитель матрицы, получаемой из матрицы R путем вычерчивания j-й строки
и l-го столбца.
Множественный коэффициент корреляции
(k - 1)-го порядка результативного признака x1
определяется по формуле
(53.4)
где | R | — определитель матрицы R.
Значимость частных и парных коэффициентов корреляции, т.е. гипотеза H
0
: ? = 0,
проверяется по
t-
критерию Стьюдента. Наблюдаемое значение критерия находится по формуле
(53.5)
где r — соответственно оценка частного или парного коэффициента корреляции
?;
l
— порядок
частного коэффициента корреляции, т.е. число фиксируемых факторов (для парного коэффициента
корреляции l=0).
Напомним, что проверяемый коэффициент корреляции считается значимым, т.е. гипотеза
H
0
: ? = 0
отвергается с вероятностью ошибки ?,
если
t
набл
по модулю будет больше, чем значение
t
кр
,
определяемое по таблицам t-распределения для заданного
?
и ? = n – l - 2.
Значимость коэффициентов корреляции можно также проверить с помощью таблиц Фишера —
Иейтса.
При определении с надежностью у доверительного интервала для значимого парного или частного
коэффициента корреляции р используют Z-преобразование Фишера и предварительно устанавливают
интервальную оценку для Z:
(53.6)

