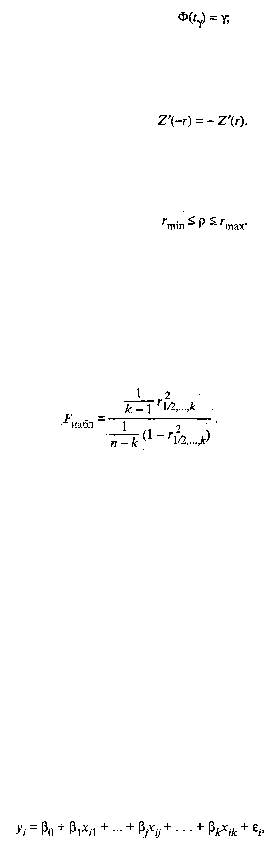
428
где t
?
вычисляют по таблице значений интегральной функции Лапласа из условия
значение
Z' определяют по таблице Z-преобразования по найденному значению r. Функция
Z'
—
нечетная, т.е.
Обратный переход от Z к
?
осуществляют также по таблице
Z-преобразования, после использования
которой получают интервальную оценку для
?
с надежностью
?:
Таким образом, с вероятностью
?
гарантируется, что генеральный коэффициент корреляции
?
будет
находиться в интервале (r
min
, r
max
).
Значимость множественного коэффициента корреляции (или его квадрата — коэффициента
детерминации) проверяется по F-критерию. Например, для множественного коэффициента корреляции
проверка значимости сводится к проверке гипотезы, что генеральный множественный коэффициент
корреляции равен нулю, т.е. H
0
: ?
1/2,…,k
= 0, а наблюдаемое значение статистики находится по формуле
(53.7)
Множественный коэффициент корреляции считается значимым, т.е. имеет место линейная
статистическая зависимость между х1 и остальными факторами х2, ..., х
k
, если F
набл
> F
кр
, где F
кр
определяется по таблице F-распределения для заданных ?, ?1 = k - 1, ?2 = n - k.
53.2. Регрессионный анализ
Регрессионный анализ — это статистический метод исследования зависимости случайной величины
у от переменных (аргументов) х
j
(j = 1, 2,..., k), рассматриваемых в регрессионном анализе как
неслучайные величины независимо от истинного закона распределения x
j
.
Обычно предполагается, что случайная величина у имеет нормальный закон распределения с
условным математическим ожиданием
y
~
= ?(x1, ..., х
k
), являющимся функцией от аргументов х
j
и с
постоянной, не зависящей от аргументов дисперсией
?
2
.
Для проведения регрессионного анализа из (k + 1)-мерной генеральной совокупности (у, x1, х2, ..., х
j
,
..., х
k
) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется значениями
переменных (у
i
,
x
i1
,
х
i2
, ..., х
ij
, ..., x
ik
), где х
ij
— значение j-й переменной для i-го наблюдения (i = 1, 2,..., n),
у
i
— значение результативного признака для i-го наблюдения.
Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид
(53.8)
где
?
j
— параметры регрессионной модели;
?
j
— случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и
дисперсию
?
2
.
Отметим, что модель (53.8) справедлива для всех i = 1,2, ..., n, линейна относительно неизвестных
параметров ?
0
, ?1,…, ?
j
, …, ?
k
и аргументов.

