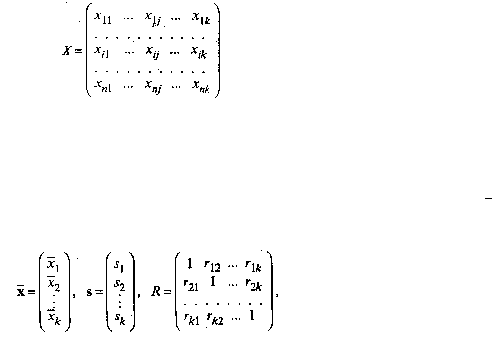
426
методов. При этом корреляционный анализ используется, с одной стороны, на этапе предварительного
анализа для выявления мультиколлинеарности, а с другой — при оценке адекватности регрессионной
модели; компонентный анализ используется в задачах снижения размерности, а также при построении
уравнения регрессии на главных компонентах и в задачах классификации. При окончательном выборе
модели рекомендуется использовать как экономические, так и статистические критерии. Наряду с
точечными оценками рассматриваются методы построения интервальных оценок коэффициентов и
уравнения регрессии.
В 53.5 «Основы эконометрики» рассматриваются производственные функции и системы
одновременных эконометрических уравнений, двухшаговый метод наименьших квадратов.
Настоящий раздел предназначен для студентов, изучающих многомерные статистические методы, и
специалистов, желающих повысить свою квалификацию в области применения современных
эконометрических методов для анализа и прогнозирования социально-экономических явлений.
Глава 53. Методы многомерного статистического анализа и моделирования социально-
экономических явлений
53.1. Корреляционный анализ
Корреляционный анализ является одним из методов статистического анализа взаимозависимости
нескольких признаков.
Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной
совокупности по выборке и определении на основе этой матрицы частных и множественных
коэффициентов корреляции и детерминации.
Парный и частный коэффициенты корреляции характеризуют тесноту линейной зависимости между
двумя переменными соответственно на фоне действия и при исключении влияния всех остальных
показателей, входящих в модель. Они изменяются в пределах от -1 до +1, причем чем ближе
коэффициент корреляции к 1, тем сильнее зависимость между переменными. Если коэффициент
корреляции больше нуля, то связь положительная, а если меньше нуля — отрицательная.
Множественный коэффициент корреляции характеризует тесноту, линейной связи между одной
переменной (результативной) и остальными, входящими в модель; он изменяется в пределах от 0 до 1.
Квадрат множественного коэффициента корреляции называется множественным коэффициентом
детерминации. Он характеризует долю дисперсии одной переменной (результативной), обусловленной
влиянием всех остальных переменных (аргументов), входящих в модель.
Исходной для анализа является матрица
размерности п х k, i-я строка которой характеризует i-е наблюдение (объект) по всем k показателям (j =
1, 2, ..., k).
В корреляционном анализе матрицу Х рассматривают как выборку объема п из k-мерной генеральной
совокупности, подчиняющейся k-мерному нормальному закону распределения.
По выборке определяют оценки параметров генеральной совокупности, а именно: вектор средних
x
,
вектор средних квадратических отклонений s и корреляционную матрицу R порядка k:

