132
принцип наименьшего времени Ферма, который был известен уже Герону и другим уч¸ным
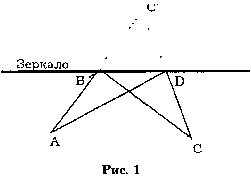
Древней Греции. Привед¸нный ниже черт¸ж, на котором указаны равные треугольники,
говорит сам за себя (рис. 1).
Если длина отрезка АВС' явно меньше длины ломаной ADC', то очевидно, что путь АВС
(равный АВС') короче и занимает меньше времени, чем любой другой путь, например путь
ADC.
Вы вправе утверждать, что, хотя представление в виде минимума является удобным, оно
ничем не лучше другого. Но пойдите после этой лекции в свою ванную комнату и
посмотрите на сво¸ отражение, опустив в воду большой палец ноги. Ваши конечности боль-
ше не будут выглядеть прямыми, поскольку скорость распространения света в воде
отличается от скорости его распространения в воздухе. Принцип наименьшего времени да¸т
вам ключ к описанию поведения света в таких условиях, а знание закона Снелла об углах —
нет. Кто теперь может сомневаться относительно того, какое из двух научных объяснений
лучше?
Пример из области экономики
Позвольте мне показать то же самое применительно к экономике, взяв в качестве
примера простейший случай. Рассмотрим фирму, стремящуюся к максимизации своей
прибыли, которая прода¸т продукцию в соответствии с кривой спроса, прич¸м цена является
невозрастающей функцией продаваемого количества. Предположим далее, что для выпуска
продукции необходимо затратить один, два или девяносто девять видов различных ресурсов.
Ради простоты будем считать, что производственная функция, связывающая объ¸мы затрат и
выпуска, является гладкой и вогнутой.
Экономист, мыслящий в стиле Маха, будучи уч¸ным-позитивистом, заинтересованным
попросту в регистрации и систематизации наблюдаемых фактов, мог бы в принципе
перенести на перфокарты информацию о 99 функциях спроса, связывающих количество
каждого ресурса, покупаемого фирмой, с 99 переменными, отражающими цены на ресурсы.
Какой, колоссальной задачей было бы хранение массивов информации, определяющих 99
различных поверхностей в стомерном пространстве! Однако на самом деле 99 поверхностей
не являются независимыми. В действительности достаточно знать единственную
"родительскую" поверхность, для того чтобы иметь возможность получить пут¸м расч¸тов
точную информацию о 99 "детях". Каким же образом становится возможной такая громадная
экономия в описании? Да в силу того факта, что наблюдаемые кривые спроса, которые
великий шведский экономист предпоследнего поколения Густав Кассель считал неделимыми
атомами в теоретическом арсенале экономиста, в действительности являются решениями
задачи максимизации прибыли! При обычных условиях регулярности эти решения
представляют собой функции, обратные семейству частных производных функции
совокупного дохода, который определяется как произведение объ¸ма продукции (при
данных объ¸мах затрат всех ресурсов) на цену спроса, по которой эта продукция будет
продана. При условии гладкости и строгой вогнутости эта "родительская" функция дохода
имеет своими "детьми" матрицу частных производных второго порядка размерности 99х99,
которая является симметричной и отрицательно определенной. Легко доказать, что эти
функции могут быть однозначно обращены в форму нового семейства "детей" с теми же

