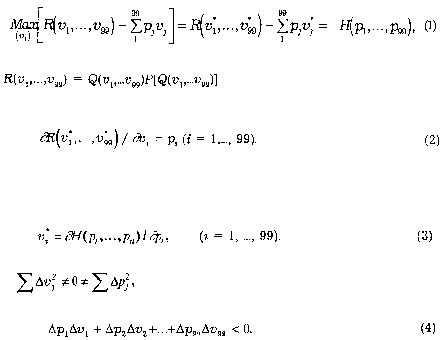
133
самыми свойствами. 99 таких "детей" не могут не иметь "родительской" функции, которую,
если бы она никогда не существовала, мы должны были бы создать, подобно Пигмалиону.
Математически это выглядит так:
где
— гладкая, строго вогнутая "регулярная функция дохода. Необходимыми условиями
максимума будут
Если, кроме того, матрица Гесса вторых частных производных является отрицательно
определ¸нной,, то уравнений (2) достаточно для максимума. Отсюда вытекают обратные
соотношения, которые могут интерпретироваться как частные производные сопряженной
функции Хотеллинга-Роя Н., а именно:
Отсюда следует, что при
наши переменные удовлетворяют неравенству
Можно сказать и больше. Хотя мне трудно представить себе характер поверхностей
даже в тр¸хмерном пространстве, я могу уверенно заявить на основе вышесказанного, что
повышение цены на любой ресурс при сохранении остальных цен постоянными определ¸нно
привед¸т к снижению спроса на этот ресурс со стороны фирмы, т.е. дv
i
/ др
i
< 0. Такой
банальный результат мог бы предвидеть любой, кто вникнет в ситуацию и спросит себя'
"Предположим, я был бы последним простаком среди предпринимателей. Что я стал бы
делать, чтобы сохранить по возможности большую прибыль в случае подорожания одного из
ресурсов?
Здесь здравый смысл и высшая математика оказываются в согласии. Однако все мы
знаем о парадоксе Гиффена, в соответствии с которым повышение цены на картофель —
основную еду бедных ирландских крестьян — может снизить их жизненный уровень на-
столько, что заставит покупать скорее больше, чем меньше картофеля. В этом случае сам
здравый смысл обнаруживается только под прожектором математики.
С помощью математики я могу видеть свойство 99-мерных поверхностей, скрытое от
простого глаза. Если повышение цены удобрений (только их одних) всегда приводит к
увеличению закупок некоей фирмой ч¸рной икры, то из одного этого факта я могу пред-
сказать результат следующего эксперимента, который никогда не проводил сам и по
которому не располагаю никакими данными наблюдений: повышение цены на одну только
икру приведет к росту закупок фирмой удобрений. В термодинамике такие условия вза-
имности или интегрируемости известны как условия Максвелла. В экономике они известны
как условия Хотеллинга — в честь Гарольда Хотеллинга, сформулировавшего их в 1932 г.
(Hotelling, 1932).
Одна из привлекательных сторон научной деятельности состоит в том, что мы все
карабкаемся на небеса на плечах своих предшественников. Экономика, подобно физике,
имеет своих героев, и букву "Н" я использовал в своих математических уравнениях не в
честь сэра Уильяма Гамильтона (Hamilton), а скорее в честь Гарольда Хотеллинга (Hotelhng).
Ведь именно его работа столь сильно вдохновляла меня, когда я начинал свою карьеру
Примерно в это же время покойный Генри Шульц пытался эконометрическими методами
проверить соответствие условии интегрируемости Хотеллинга эмпирическим данным
(Schultz, 1938).

