52
Закон двойного отрицания:
не (не А) = А.
Отрицание отрицания равносильно исходному утверждению.
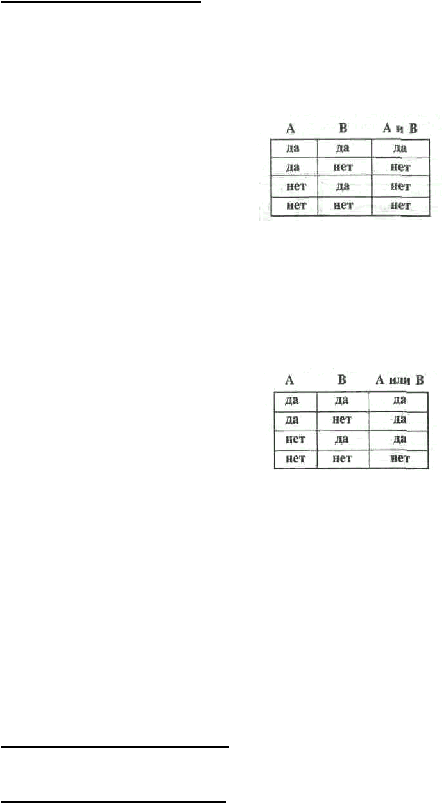
Логическая связка и в математической логике называется конъюнкцией. Таблица истинности
конъюнкции:
Свойства конъюнкции:
И1: Конъюнкция А и В истинна, когда истинны оба суждения.
И2: Конъюнкция А и В ложна, когда ложно хотя бы одно из суждений А или В.
Логическая связка или в математической логике называется дизъюнкцией. Таблица истинности
дизъюнкции:
Свойства дизъюнкции:
ИЛИ1: Дизъюнкция А или В истинна, когда истинно любое из суждений А или В.
ИЛИ2: Дизъюнкция А или В ложна, когда ложны оба суждения А и В.
Для понимания принципов поиска информации по запросам в базах данных и сети Интернет
необходимо понимать математический смысл сложносоставных запросов с использованием логических
операций «И» (AND), «ИЛИ» (OR) и «НЕ» (NOT).
Примеры сложносоставных запросов к базам данных и их эквивалентные позитивные
переформулировки:
(признак
? 0)
& не (х > 0)
? (
признак (0))
& (х
?0);
(число > 0) v не (у > 0)
? (
число > 0)
v (у
? 0).
Общие принципы отрицания дизъюнкций и конъюнкций в математической логике выражаются
двумя закона де Моргана:
Закон отрицания конъюнкции:
не (А и В) = (не А) или (не В)
— отрицание конъюнкции суждений равносильно дизъюнкции отрицаний.
Закон отрицания дизъюнкции:
не (А или В) ((не А) и (не В))
— отрицание дизъюнкции суждений равносильно конъюнкции отрицаний.
Знание и использование данных трех общих законов логики позволяют полностью избавляться от
негативных формулировок в запросах к базам данных и в общении друг с другом. Но еще важнее
знание этих законов для понимания принципов и результатов поиска информации компьютерами.
Попробуйте проверить законы отрицания в запросах к Интернет и объясните результаты,
полученные от различных поисковых систем:
запрос: «учебник -физика» — «учебник, но не по физике?»
запрос: «учебник -книга» — «учебник, но не книга?»

