51
доказательствах и обоснованиях, чем они отличаются от обычных нормальных людей. И на них нельзя
обижаться.
Отличие вычислительных операций и математических суждений от обычных человеческих действий
и высказываний состоит в следующем. Вычислительные операции и математические суждения всегда
предполагают однозначную интерпретацию, в то время как действия и высказывания людей зачастую
допускают многозначную художественную трактовку.
Суждения и в математике, и на практике могут быть истинными или ложными. На практике
истинность или ложность суждений проверяется их соответствием действительности, а в математике —
опровержениями либо доказательством.
Пример истинного суждения —
«снег белый». Пример ложного суждения —
«генетика —
лженаука». Пример суждений, истинность которых до сих пор до конца еще не установлена: «машина
может думать», «на Марсе есть жизнь», «информатика — наука».
Работа ЭВМ как автоматических устройств основана исключительно на однозначных правилах
выполнения команд, программ и алгоритмах обработки данных. Тем самым работа компьютеров, а
также всех вычислительных устройств, систем и сетей допускает верификацию — строгую
однозначную проверку правильности их работы.
Все сложные логические элементы и блоки вычислительных машин и устройств конструируются из
простейших логических элементов с помощью логических операций «И» (AND), «ИЛИ» (OR) и «НЕ»
(NOT). В математической логике для этих операций обычно используются обозначения — & («И»), V
(«ИЛИ») и — («НЕ»).
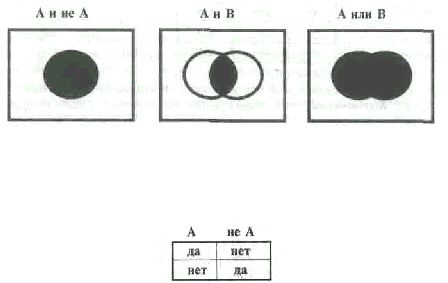
Наглядной иллюстрацией этих логических связок служат следующие диаграммы:
Отрицание не А истинно или ложно в зависимости от истинности исходного суждения А. Свойства
отрицания не как логической связки можно описать таблицей истинности:
Таблица истинности:
Свойства отрицаний:
НЕ1: Отрицание ложно, если суждение истинно.
НЕ2: Отрицание истинно, если суждение ложно.
Для понимания роли отрицаний в языках запросов важно уметь выражать их в позитивной форме.
Приведем примеры отрицания математических неравенств и их эквивалентные позитивные
переформулировки:
не (х = 0)
? (
х
? 0);
не (х
? 0)
? (
х = 0);
не (х > 0)
? (
х
? 0);
не (х < 0)
? (
х
? 0);
не (х
? 0) ? (
х < 0);
не (х
? 0) ? (
х > 0).
Для общего понимания математических суждений, утверждений и отрицаний необходимо иметь
представления об
общих законах математики и математической логики в частности. Первым среди
общих законов математической логики явлется

