53
запрос: «-учебник информатика» — «не учебник, но по информатике?»
запрос: «-(-учебник)» — «неверно, что это не учебник» ??? .
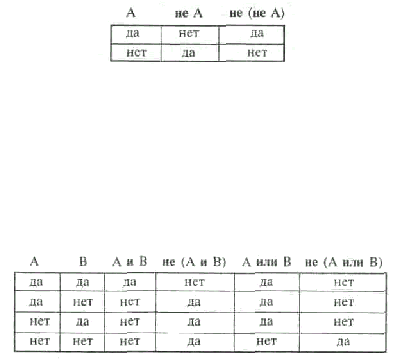
Задача 1. Проверьте закон двойного отрицания не (не А)
?
А с помощью таблиц истинности.
Сравнение крайних столбцов показывает, что всюду, где высказывание А истинно, там же истинно и
двойное отрицание не (не А). И наоборот, всюду, где ложно А, там ложно и двойное отрицание не (не
А). Следовательно, двойное отрицание тождественно исходному высказыванию: не (не А)
?
А.
Задача 2. Сравните с помощью таблиц истинности отрицание дизъюнкции и отрицание конъюнкции
не (А и В) и не (А или В).
Решение.
Вопросы
1. Что такое дизъюнкция?
2. Что такое конъюнкция?
3. Когда истинно отрицание?
4. Когда ложно отрицание?
5. Когда истинна конъюнкция?
6. Когда истинна дизъюнкция?
7. Чему соответствует отрицание отрицания?
8. Чему соответствует отрицание конъюнкции?
9. Чему соответствует отрицание дизъюнкции?
Задания
1. Проверьте запросы с отрицаниями в Интернет и объясните полученные результаты:
запрос: «-(-интернет)»
запрос: «поиск -интернет»
запрос: «поиск информации -интернет»
запрос: «информатика -Ершов»
2. Составьте таблицы истинности для утверждений:
а) (не А) и (не В);
б) (не А) или (не В);
в) А и (не В);
г) А или (не В).
3. Сравните с помощью таблиц истинности логические выражения:
а) не (А и В) и (не А) или (не В);
б) не (А и В) и (не А) или (не В);
в) не (А) и В и А и (не В);
г) не (А) или В и А или (не В).
4. Проверьте по таблицам истинности логические законы:
а) отрицание конъюнкции:

