118
Другими словами, можно считать величины R
t
, О
t
и В
t
детерминированными, однако для их
определения можно было бы применить и статистические методы, описанные в гл. 10.
Перейдем к процессам расходования воды, один из них – испарение. С достаточной точностью
можно считать, что I
t
?
D
t
, где D
t
– дефицит влажности, который может быть рассчитан так же, как
выражения (12.1)–(12.3) по данным наблюдений. Тогда
I
t
= ?D
t
,
(12.4)
где ? – эмпирический коэффициент пропорциональности.
Далее, объем воды F
t
, которая профильтровывается в нижнем створе водохранилища,
пропорциональна объему воды в водохранилище, т. е.
F
t
= kX
t
,
(12.5)
где k
– эмпирический коэффициент пропорциональности, соответствующий определенному типу
грунта.
Расход воды через плотину Р
t
– величина регулируемая. Регулируемыми величинами являются
величины потребления S
t
и К
t
, которые суммарно обозначим через Q
t
, т. е.
Q
t
= S
t
+ K
t
(12.6)
Итак, после рассмотрения всех процессов формирования воды в водохранилище можно записать
закон сохранения массы воды:
X
t+?t
= x
t
+ Y
t
– Z
t
,
(12.7)
где
Y
t
= R
t
+ O
t
+ В
t
,
(12.8)
Z
t
= I
t
+ F
t
+ P
t
+ Q
t
.
(12.9)
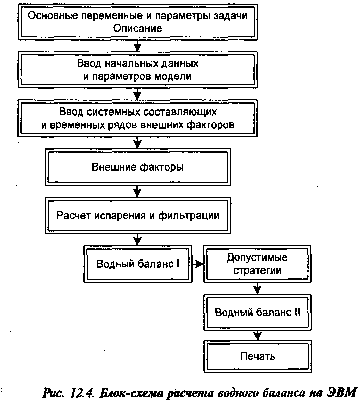
Эти уравнения часто называют уравнениями баланса. Задавая условия накопления и расходования
воды и решая уравнения водного баланса, можно получить ответ на поставленный вопрос: чему равен
запас воды в водохранилище в каждый момент времени t. Блок-схема соответствующего расчета на
ЭВМ приведена на рис. 12.4.
Прокомментируем значения отдельных фрагментов программных блоков.
Блок «Внешние факторы» с шагом в один месяц прогнозирует значения внешних факторов по
заданным временным рядам.
Следующий блок, используя прогнозные значения внешних факторов, осуществляет вычисление
воды, испарившейся и профильтровавшейся из водохранилища. Блок «Водный баланс I» вычисляет

