108
n
i
i
p
1
.
1
(11.15)
Кроме того, очевидно, что задача g(x)
>
max эквивалентна задаче (-g(x))
>
min; также очевидно, что
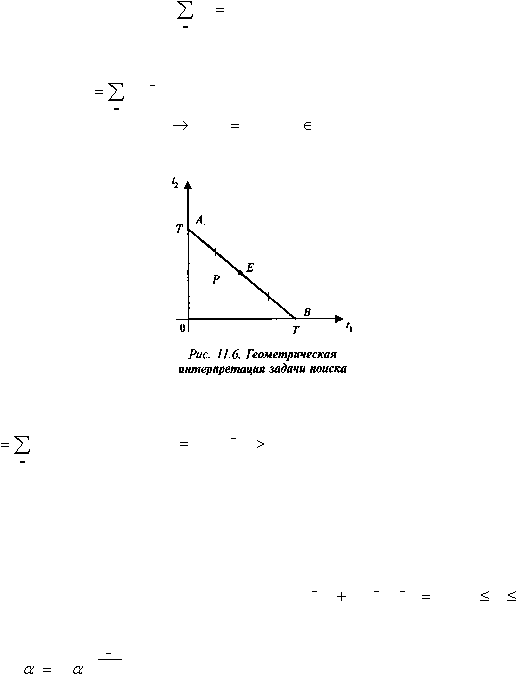
условия (11.13) и (11.14) определяют определенный полиэдр Р (рис. 11.6). Следовательно, вводя
целевую функцию
,
)
,...,
(t
1
1
n
i
t
a
i
n
i
i
e
p
t
f
получаем следующую оптимизационную задачу:
P
t
t1
t
t)
f
n
)
,...,
(
min,
(
, (11.16)
где Р– полиэдр, заданный неравенствами (11.13) и (11.14).
Так как
),
(t
)
(t
1
i
n
i
i
f
f
причем
0
)
(t
2
"
i
i
t
a
i
i
i
i
e
a
p
f
, то функция f(t) выпуклая и мы имеем задачу
выпуклого программирования. Общие методы решения таких задач довольно сложны, однако в нашем
конкретном случае можно предложить наглядное геометрическое решение.
Действительно, имеем
)
(t
'
i
i
f
<0. Значит, функция f(t) убывает по любому переменному t
i
,
i = 1, 2,...,n,
и ее наименьшее значение достигается на гиперплоскости t1 + t2 +…+ t
n
=
T
(в случае двух переменных
это прямая АВ на рис. 11.6). Однако в отличие от задач линейного программирования это наименьшее
значение достигается необязательно в вершинах А, В и т.д., в чем можно убедиться, исследуя на АВ
функцию f(t) в случае двух переменных. Тогда f(t1,t2)=
.
0
),
(t
1
1
)
(T
2
1
1
2
1
1
T
t
h
e
p
e
p
t
a
t
a
Минимум
этой функции может достигаться и внутри отрезка [0, T] в зависимости от соотношения параметров р1,
р2, ?1, ?2, в чем можно убедиться непосредственным исследованием функции одного переменного
(например, если
,
2
2
2
1
1
2
1
T
a
a
e
p
p
то минимум достигается в середине Е отрезка АВ).
11.3. Игровые модели
Часто возникают ситуации, в которых различные участники имеют не совпадающие между собой
интересы. Математические модели и методы для исследования таких так называемых конфликтных
ситуаций получили название теории игр [18].
Приведем простейшие понятия и результаты этой теории. Под словом «игра» понимается
совокупность правил, руководствуясь которыми игроки-участники принимают решения. Предположим,
что результатом игры является плата, которую в соответствии с правилами проигравший участник
платит выигравшим. Для простоты ограничимся сначала так называемыми «играми двух лиц с нулевой
суммой». Для того чтобы полностью определить такую игру, нужно задать таблицу платежей –
платежную матрицу, например, следующую матрицу размера 3х4:

