106
11.2. Задача поиска
Более сложными, чем задачи линейного программирования, являются задачи выпуклого
программирования. Прежде чем привести пример такой задачи, связанной с безопасностью
жизнедеятельности, дадим некоторые определения из теории выпуклого анализа [39].
Определение 1.
Множество Х из пространства R
n
называется выпуклым, если из того, что две
точки у и z принадлежат этому множеству, вытекает, что и весь отрезок {у,z}={х
R
n
:х=
у+(1-
)z,
0
1, соединяющий эти точки, также принадлежит этому множеству.
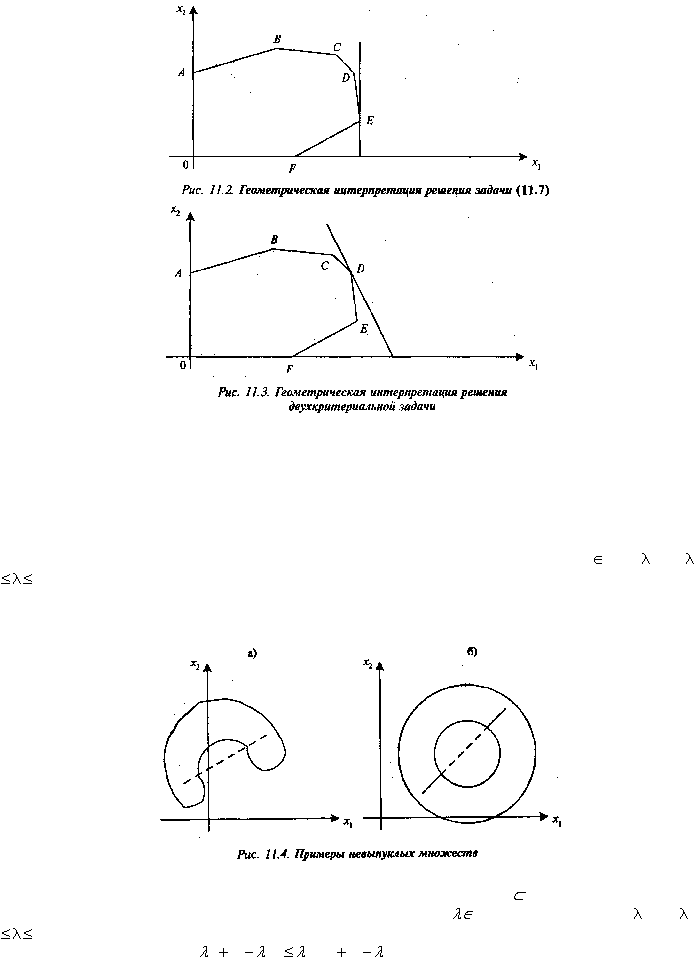
Очевидным примером выпуклых множеств является внутренность круга, шара, эллипсоида, куба. На
рис. 11.4 а, б приведены примеры невыпуклых множеств на плоскости R².
Определение 2. Функция f(x), определенная на выпуклом множестве x
R
n
, называется выпуклой,
если для любых двух точек у и z, принадлежащих X, и любого
x[0,1] (тогда отрезок [
y+(1-
)z],
0
1, целиком принадлежит X) выполняется неравенство
)
(
)
1
(
)
(
)
1
(
(
z
f
y
f
z
y
f
,
(11.9)
Замечание. Если неравенство (11.9) имеет противоположный знак, то функция f(x) называется
вогнутой.

