101
где y(t)
– случайная величина со средним значением, равным нулю. Решение задачи (уравнения
(10.15) при условии (10.16)) имеет вид
t
d
y(
at
e
N
t)
N
0
)
0
(
. (10.17)
Чтобы придать смысл интегралу
t
d
y(
0
)
от случайной величины y(t), сделаем некоторые
упрощающие предположения. Будем считать, что y(t) – ступенчатая функция: y(t)=y
i
, при i-1
?
t?i,
i=1,2,.... при этом все случайные величины у, имеют нормальное распределение [6]. Нормальный закон
распределения (часто называемый законом Гаусса) наиболее часто встречается на практике.
Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений,
могут быть представлены как суммы большого числа сравнительно малых слагаемых – элементарных
ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким
бы законам распределения ни были подчинены элементарные ошибки, особенности этих распределений
в сумме большого числа слагаемых нивелируются, а сумма оказывается подчиненной закону, близкому
к нормальному. Например, проводя измерения длины листьев, упавших с деревьев в лесу, мы имеем
случайную величину Х – длину листьев. Вероятность того, что Х<х, т. е. Р={Х <х}, называется
функцией распределения случайной величины и обозначается через F(x), а ее производная F'(x) = f(x)
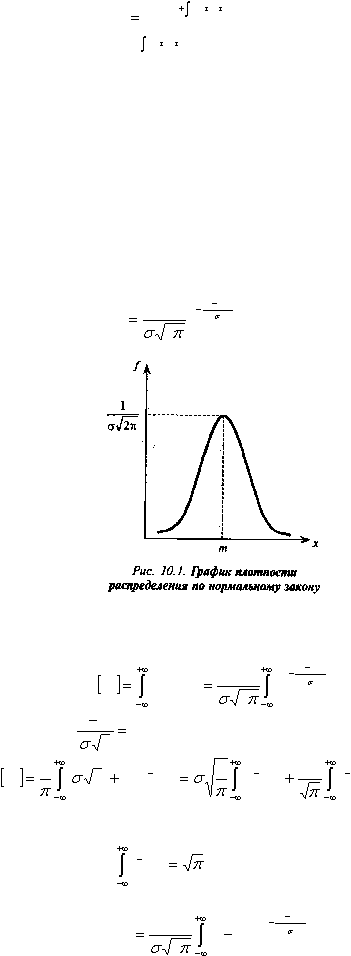
называется плотностью распределения и в случае нормального закона распределения имеет вид (рис.
10.1)
2
2
)2
(x
2
1
)
(x
m
e
f
. (10.18)
Численные параметры т и
?
– это математическое ожидание (среднее значение) и среднее
квадратичное отклонение случайной величины X. Действительно,
.
2
1
)dx
(
2
2
2
)
(
dx
xe
x
xf
X
M
m
x
Применяя замену переменной
t
m
x
2
, получаем
.
2
)e
2t
(
1
2
2
2
t
t
t
e
m
dt
te
dt
m
X
M
(10.19)
Нетрудно убедиться, что первый из двух интегралов в уравнении (10.19) равен нулю, а второй
представляет собой известный интеграл Эйлера–Пуассона
dt
e
t2
, (10.20)
поэтому из уравнения (10.19) вытекает, что М[Х]=т. Вычислим дисперсию величины X:
.
)
(x
2
1
]
[x
2
2
2
)
(x
2
dx
e
m
D
m

