76
МП = МR - МС.
(5.15)
Предприятие максимизирует прибыль, продолжая выпуск до того объема, при котором предельная
выручка будет равняться предельным затратам: MR = МС. Можно увидеть это, приравняв предельную
прибыль нулю в уравнении (5.15).
Поскольку для конкурентного предприятия цена равна предельной выручке, максимальная прибыль
для него получится тогда, когда выпуск установится в точке, где предельные затраты сравняются с
рыночной ценой, то есть:
МС = Р.
(5.16)
Объединив уравнения (5.14) и (5.16), получим:
MC = MR
P.
(5.17)
Таким образом, равновесный выпуск максимизирующего прибыль конкурентного предприятия – это
выпуск, при котором предельные затраты равны предельной выручке (причем последняя тождественна
цене товара). Иными словами, в этом случае достигается оптимум конкурентного предприятия.
Равенство МС = Р является условием первого порядка для определения оптимума конкурентного
предприятия.
Графически оптимум конкурентного предприятия показан на рис.
5.13 и 15.14. На рис. 5.13, а
приведен график общей выручки TR и общих затрат предприятия в коротком периоде в условиях
современной конкуренции. При неизменных ценах кривая TR – это луч, проведенный из начала
координат с наклоном:
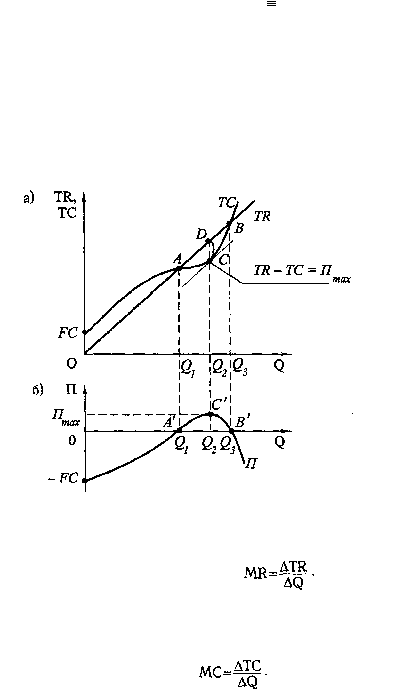
Рис. 5.13. График общей выручки, общих затрат и прибыли конкурентного предприятия при
неизменном уровне цен
(5.18)
Итак, наклон кривой общей выручки равен предельной выручке, которая, в свою очередь, равна
рыночной цене товара, продаваемого конкурентным предприятием.
С другой стороны, наклон кривой общих затрат ТС составит в любой точке:
(5.19)
При любом объеме выпуска прибыль будет равна разнице по высоте между кривыми общей выручки
и общих затрат. Следует отметить, что в точках А и B
TR = ТС и, следовательно, прибыль у
предприятия будет отсутствовать, то есть П = 0 (точки А и В называются, как известно, точками
безубыточности). Hа рис. 5.13, б точкам безубыточности соответствуют точки А' и В'.

