223
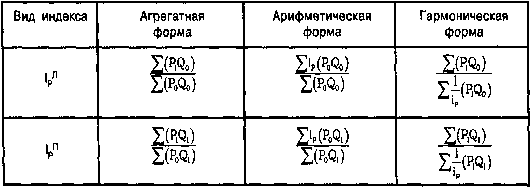
Преимущества агрегатной формы – в ее ясном экономическом смысле. Она устанавливает изменение
цен при предположении, что количества товаров неизменны, при этом в формуле Ласпейреса берется
количество проданного товара в базисном периоде (Q
0
), а в формуле Пааше – в текущем (Q1).
Среднеарифметическая форма не имеет такого ясного экономического смысла, но ее преимущества
состоят в том, что она позволяет более легко производить сам расчет индекса и облегчает последующие
его перерасчеты. В частности, при расчете по среднеарифметической взвешенной формуле с базисными
весами (формула Ласпейреса) значительно легче установить веса, достаточно иметь данные о стоимости
продаж указанных товаров в базисный период, то есть P
0
Q
0.
Поэтому индексы цен в большинстве развитых стран строятся по среднеарифметической взвешенной
формуле Ласпейреса.
В отечественной статистике до 1992 г. общий индекс цен рассчитывался по формуле Пааше,
используя гармоническую его форму. Связано это было с простотой получения данных о текущем
товарообороте (P1Q1) в связи со сплошной ежемесячной статистической отчетностью и незначительным
изменением цен. Однако после 1992 г., когда был осуществлен переход к рыночным отношениям и
принята новая методика расчета индекса потребительских цен, он стал рассчитываться так же, как и в
большинстве стран, по формуле Ласпейреса.
Статистическим анализом доказано, что в долговременном аспекте формула Пааше занижает
реальное изменение цен вследствие отрицательной корреляции проданного количества товара и цены, а
в случае долгосрочных и международных сопоставлений разница между индексами, взвешенными
разными способами, составляет несколько процентов. Значения индексов, вычисленных по формулам
Ласпейреса и Пааше, совпадают лишь в случае почти невозможного на практике совпадения структуры
товарной массы базисного и отчетного периодов.
Теоретически и формула Ласпейреса, и формула Пааше имеют определенный экономический смысл.
Каждая из них может использоваться в соответствии с той или иной экономической задачей.
Четкость интерпретации, экономический смысл и удобство практического расчета формулы
Ласпейреса сделали ее очень популярной в мире для расчета индекса потребительских цен (ИПЦ),
который показывает, во сколько раз изменились бы потребительские расходы в текущем периоде по
сравнению с базисным, если бы при изменении цен уровень потребления оставался прежним.
Другой важный показатель – дефлятор валового национального продукта в большинстве стран
рассчитывается по формуле Пааше, и тем самым расчет максимально приближен к совокупности
товаров, произведенных в отчетном периоде.
В связи с расхождениями в результатах между индексами с текущими и базисными весами возникла
теория о так называемых весовых отклонениях (weightbins). Суть ее сводится к утверждению, что
использование и текущих и базисных весов ведет к отклонениям в величине индекса от его истинного
значения, в первом случае в сторону понижения, а во втором – повышения. Поэтому задача теории
индексов состоит в разработке таких формул индексов, которые ликвидировали бы эти отклонения и
дали бы результаты, свободные от влияния использования весов за различные периоды.
Однако в данном случае рассматривается не экономическое содержание индексов, а определенные
формальные требования к ним. С позиции экономического содержания одинаково правомерны индексы
цен с использованием и базисных и текущих весов. Расхождения между их величинами не есть
результат каких-то противоположных отклонений от единственно правильной величины. Правомерен и
более высокий результат, полученный на основе формулы Ласпейреса, и более низкий результат,

