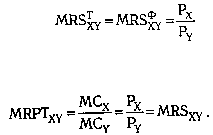
146
дополнительной единицы товара Х при полном и эффективном использовании всех ресурсов.
Геометрически MRPT
XY
представляет собой тангенс угла наклона касательной к границе
производственных возможностей, взятый с противоположным знаком. (Проведенная через точку R
касательная на рис. 9.5 и характеризует MRPT.) Предположим, что в точке R – МRРТ
XY
= 1,2.
Теперь сделаем еще один шаг: наложим на множество производственных возможностей коробку
Эджуорта-Боули для двух потребителей таким образом, чтобы совместить начало координат для
Трифона с точкой О, а начало координат для Федора – с точкой R. Кривая OR представляет собой
контрактную линию. Рассмотрим распределение двух благ между потребителями, соответствующее
точке С. Это распределение принадлежит контрактной линии. Находясь в этой точке, Трифон из общего
количества в 70 единиц блага Х получает 30 единиц блага X, а Федор – 40. Из общего количества блага
Y в 50 единиц Трифон получает 30 единиц, а Федор – 20. Как было уже сказано, все точки,
принадлежащие контрактной линии, являются точками касания двух кривых безразличия этих
потребителей и при этом предельные нормы замены у них равны. Предположим, что в точке С
предельные нормы замены для двух кривых безразличия равны 0,6: MRS
Ф
XY
= MRS
T
XY
= 0,6. Из рисунка
видно, что касательная к кривой безразличия, проведенная через точку С, имеет меньший наклон, чем
касательная к границе производственных возможностей, которая проведена через точку R.
Таким образом, при объемах производства, соответствующих точке R, и при распределении данной
продукции между потребителями, соответствующем точке С, достигается как эффективность в
производстве, так и эффективность в распределении. Однако достигается ли при этом Парето-
оптимальное состояние? Ответ: нет. Для доказательства этого зафиксируем количество товаров Х и Y,
потребляемое Федором. Далее сократим производство Х на единицу. Поскольку MRPT
XY
= 1,2, то это
позволит увеличить производство Y на 1,2 единицы. А поскольку MRS
XY
= 0,6, то Трифон согласится в
обмен на сокращение продукта Х на единицу получить дополнительно только 0,6 единиц продукта Y.
Его благосостояние при этом не изменится. Если же он получит 1,2 единицы блага Y, его
благосостояние повысится. Следовательно, если предельная норма продуктовой трансформации не
равна предельной норме замены какого-либо из потребителей, то можно увеличить благосостояние
одного из них, не ухудшая положения другого, с помощью изменения структуры выпуска данной
продукции. Для данной ситуации это можно сделать, сокращая объем производства блага Х и
увеличивая объем производства Y, то есть, двигаясь по границе производственных возможностей (рис.
9.5).
Таким образом, необходимым условием эффективности структуры выпуска продукции, а
также Парето-оптимальности является равенство:
MRPT
XY
= MRS
T
XY
= MRS
Ф
XY
.
(9.7)
Что произойдет, если мы будем рассматривать модель с n продуктами и m потребителями?
Очевидно, что данное равенство (9.7) должно выполняться для любой пары продуктов и для всех
потребителей.
Замечание. В данном упрощенном случае мы рассмотрели только три необходимых условия Парето-
оптимальности. Если же рассматриваются более сложные ситуации (например, возможность
изменения объемов производственных ресурсов), то в этом случае формулируются дополнительные
признаки Парето-оптимального состояния.
Поскольку у разных потребителей различные предпочтения благ, то весьма трудно определить,
сколько благ нужно произвести и сколько дать каждому потребителю, чтобы у всех была одинаковая
MRS? Для этого нужны значительные информационные и материально-технические затраты. Данную
проблему проще решить следующим образом.
Если рынки благ являются совершенно конкурентными, все потребители распределят свой бюджет
так, чтобы предельные нормы замены по товарам равнялись отношению цен:
(9.8)
В то же время каждая фирма, максимизирующая прибыль, будет продолжать выпуск до тех пор,
пока цена не сравняется с предельными издержками, то есть P
X
= МС
X
и P
Y
= МС
Y
. Следовательно:
(9.9)

