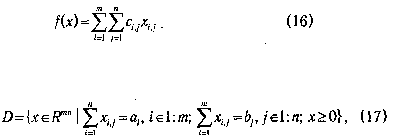
8
системе примут вид:
Функция (16) и описанные выше ограничения, записанные в форме
задают транспортную модель. На ее основе может быть сформулирована задача минимизации
суммарных затрат на перевозки:
f(x)=cx > min, x? D, (18)
которая в литературе получила название транспортной задачи в матричной постановке. Вообще
говоря, транспортная задача является частным случаем задачи (11), но в силу ряда особенностей для ее
решения применяются специфические методы, которые, помимо прочего, позволяют прийти к важным
теоретическим обобщениям.
Общим для рассмотренных выше задач является то, что в них стоит проблема поиска наибольшего
или наименьшего (оптимального) значения некоторой функции, отражающей цель управления
системой, или, как еще говорят, целевой функции. Поиск оптимального значения осуществляется на
некотором подмножестве допустимых значений переменных, описывающих состояние этой системы,
именуемом множеством допустимых планов.
Пусть на некотором множестве D определена функция f(x). Напомним, что точка х*, принадлежащая
D (х*? D), называется точкой глобального максимума, если для любого x?
D выполняется
неравенство f(x)
? f(x*).
В этом случае значение f(x*) называется глобальным максимумом функции.
Точка ??? называется точкой локального максимума, если существует некоторая окрестность этой
точки, в любой точке которой значение функции меньше, чем в ??? (f(x) ? f([??)). По аналогии, с точностью
до знака неравенства, определяются глобальный и локальный
минимумы. Обобщающим понятием
для максимума и минимума является таксой термин, как экстремум (оптимум).
Необходимо отметить, что далеко не всегда весь комплекс целей и задач, стоящий перед
моделируемым объектом, может быть выражен в форме некоторой целевой функции. Более того,
осознание и осмысление этой проблемы стало своего рода переломным этапом в истории развития
исследования операций как науки, положившим конец многим необоснованным ожиданиям и
одновременно давшим толчок к развитию новых направлений, связанных с методами
многокритериальной оптимизации. Однако следует иметь в виду, что все они базируются на
фундаменте методов однокритериальной оптимизации, без ясного понимания которых невозможна
работа с более сложным математическим аппаратом.
Как уже отмечалось выше, работа с данной книгой предполагает знакомство читателя с
классическими методами поиска экстремума, основывающимися на аппарате дифференциального
исчисления. Но непосредственное применение классических методов для оптимизации функций,
зависящих от большого числа переменных, при наличии значительного количества ограничений
наталкивается на серьезные вычислительные трудности, что делает соответствующий аппарат
неэффективным.
Мощным инструментом разрешения подобного рода задач стали специальные методы поиска
экстремума, составляющие содержание раздела исследования операций, который называется
математическое программирование. В данном случае понятие программирование употребляется в
смысле планирование (в отличие от программирования для ЭВМ).
В свою очередь, в зависимости от вида решаемых задач, в математическом программировании
выделяют такие области, как линейное, нелинейное, дискретное, динамическое, геометрическое,
стохастическое программирование. Первые четыре раздела, а также их применение для решения
экономических задач составили содержание последующих глав.
ГЛАВА 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

