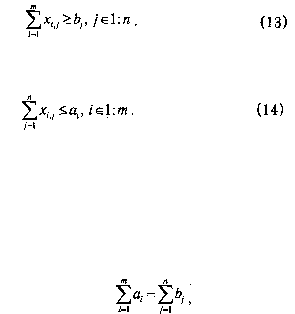
7
методов решения является их универсальность, поскольку к модели (11) могут быть сведены очень
многие как экономические, так и неэкономические проблемы.
Поскольку любая научная модель содержит упрощающие предпосылки, для корректного применения
полученных с ее помощью результатов необходимо четкое понимание сути этих упрощений, что, в
конечном счете, и позволяет сделать вывод об их допустимости или недопустимости. Наиболее
«сильным» упрощением в рассмотренной модели является предположение о прямо пропорциональной
(линейной) зависимости между объемами расхода ресурсов и объемами производства, которая задается
с помощью норм затрат а
i,j
. Очевидно, что это допущение далеко не всегда выполняется. Так, объемы
расхода многих ресурсов (например, основных фондов) изменяются скачкообразно в зависимости от
изменения компонентов объема производства х. К другим упрощающим предпосылкам относятся
предположения о независимости цен с
j
от объемов х
j
, что справедливо лишь для определенных
пределов их изменения, пренебрежение эффектом кооперации в технологиях и т. п. Данные «уязвимые»
места важно знать еще и потому, что они указывают принципиальные направления совершенствования
модели.
Транспортная задача. Рассмотрим проблему организации перевозки некоторого продукта между
пунктами его производства, количество которых равно m, и n пунктами потребления. Каждый i-й пункт
производства (i? 1:m) характеризуется запасом продукта а
i
? 0,
а каждый
j-и пункт потребления (j ? 1:
n) — потребностью в продукте b
j
? 0.
Сеть дорог, соединяющая сис
тему рассматриваемых пунктов,
моделируется с помощью матрицы С размерности m на n, элементы которой с
i,j
представляют собой
нормы затрат на перевозку единицы груза из пункта производства
i в пункт потребления j. План
перевозки груза в данной транспортной сети представляется в виде массива элементов размерности m х
n:
х = (x
1,1
…x
1,n
, x
2,1
….,x
2,n
,… , x
i,1
, …, x
i,n
,…, x
m,1
,…,x
m,n
). (12)
В (12) план перевозок х может рассматриваться как вектор, распадающийся на m групп, по n
элементов в каждой, причем i-я группа соответствует объемам груза, вывозимым из j-го пункта
производства во все возможные пункты потребления. Если реальная перевозка между пунктами i и j
отсутствует, то полагают х
i,j
= 0.
Ограничения на возможные значения х ? R
mn
имеют вид:
1.
Ограничение на удовлетворение потребностей во всех пунктах потребления:
2. Ограничения на возможности вывоза запасов из всех пунктов производства:
3. Условия неотрицательности компонентов вектора плана:
х, х
i,j
?
0, i ? l : m, j ? l : n. (15)
Существенной характеристикой описываемой модели является соотношение параметров а
i
и b
j
. Если
суммарный объем производства равен суммарному объему потребления, а именно,
то система называется сбалансированной. При выполнении условия сбалансированности разумно
накладывать такие ограничения на суммарный ввоз и вывоз груза, при которых полностью вывозится
весь груз и не остается неудовлетворенных потребностей, т. е. условия (13) и (14) приобретают форму
равенств.
По аналогии с задачей производственного планирования предположим, что затраты на перевозку
прямо пропорциональны количеству перевозимого груза. Тогда суммарные затраты на перевозку в

