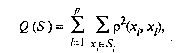
445
Существует большое количество различных способов разбиения заданной совокупности элементов
на классы. Поэтому представляет интерес задача сравнительного анализа качества этих способов
разбиения Q(S), определенного на множестве всех возможных разбиений.
Тогда под наилучшим разбиением S* понимаем такое разбиение, при котором достигается экстремум
выбранного функционала качества. Следует отметить, что выбор того или иного функционала качества,
как правило, опирается на эмпирические соображения.
Рассмотрим наиболее распространенный функционал качества разбиения. Пусть исследователем
выбрана метрика
?
в пространстве
Х и пусть S = (S1, S2,..., S
p
) — некоторое фиксированное разбиение
наблюдений x1, ..., x
n
на заданное число p классов S1, S2, ..., S
p
.
За функционал качества берут сумму («взвешенную») внутриклассовых дисперсий
(53.51)
где x
l
— вектор средних для l-го кластера.
Иерархические кластер-процедуры
Иерархические (древообразные) процедуры являются наиболее распространенными (в смысле
реализации на ЭВМ) алгоритмами кластерного анализа. Они бывают двух типов: агломеративные и
дивизимные. В агломеративных процедурах начальным является разбиение, состоящее из п
одноэлементных классов, а конечным — состоящее из одного класса; в дивизимных — наоборот.
Принцип работы иерархических агломеративных (дивизимных) процедур состоит в
последовательном объединении (разделении) групп элементов, сначала самых близких (далеких), а
затем — все более отдаленных (близких) друг от друга. Большинство этих алгоритмов исходит из
матрицы расстояний.
К недостаткам иерархических процедур следует отнести громоздкость их численной реализации.
Алгоритмы требуют вычисления матрицы расстояний на каждом шаге, а следовательно, емкой
машинной памяти и большого количества времени. В этой связи реализация таких алгоритмов при
числе наблюдений, большем нескольких сотен, нецелесообразна, а в ряде случаев и невозможна.
В качестве примера рассмотрим агломеративный иерархический алгоритм. На первом шаге
алгоритма каждое наблюдение x
i
(i = 1, 2, ..., п) рассматривается как отдельный кластер. В дальнейшем
на каждом шаге работы алгоритма происходит объединение двух самых близких кластеров, и с учетом
принятого расстояния по формуле пересчитывается матрица расстояний, размерность которой,
очевидно, снижается на единицу. Работа алгоритма заканчивается, когда все наблюдения объединены в
один класс.
Большинство программ, реализующих алгоритм иерархической классификации, предусматривает
графическое представление результатов классификации в виде дендрограммы.
Пример. Классификация стран по уровню жизни населения
В табл. 53.4 представлены значения следующих шести показателей, характеризующих условия жизни
населения двадцати стран в 1994 г.:
x1 — потребление мяса и мясопродуктов на душу населения (кг);
х2 — смертность населения по причине болезни органов кровообращения на 100 тыс. человек;
х3
— оценка валового внутреннего продукта по паритету покупательной способности в 1994 г. на душу
населения (в % по отношению к США);
x
4
— расходы на здравоохранение (в % от ВВП);
x
5
— потребление фруктов и ягод на душу населения (кг);
x
6
— потребление хлебопродуктов на душу населения (кг).
Провести классификацию стран по уровню жизни населения и дать содержательную интерпретацию
полученных результатов.
Таблица 53.4

