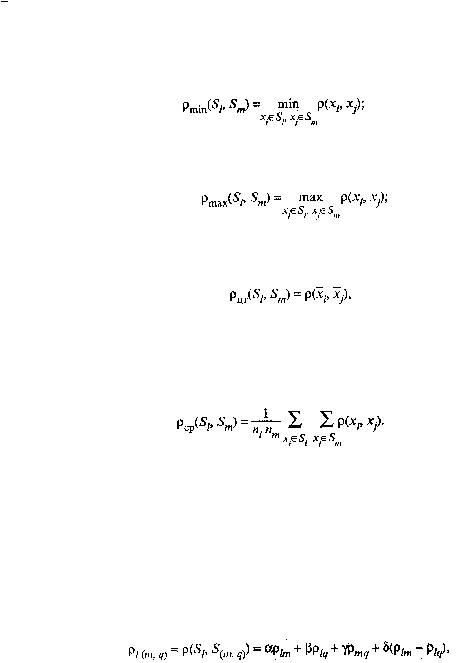
444
и равно числу несовпадений значений соответствующих признаков в
рассматриваемых i-м и
j-м
объектах.
Как правило, решение задач классификации многомерных данных предусматривает в качестве
предварительного этапа исследования реализацию методов, позволяющих выбрать из k исходных
признаков x1, x2, ..., x
k
сравнительно небольшое число наиболее информативных, т.е. уменьшить
размерность наблюдаемого пространства.
В ряде процедур классификации (кластер-процедур) используют понятия расстояния между
группами объектов и меры близости двух групп объектов.
Пусть S
i
— i-я группа (класс, кластер), состоящая из n
i
объектов;
i
x
— среднее арифметическое векторных наблюдений группы S
i
, т.е. «центр тяжести»;
?(S
l
,
S
m
) — расстояние между группами S
l
и S
m
.
Наиболее употребительными расстояниями и мерами близости между классами объектов являются:
•
расстояние, измеряемое по принципу «ближайшего соседа»:
(53.46)
•
расстояние, измеряемое по принципу «дальнего соседа»:
(53.47)
•
расстояние, измеряемое по «центрам тяжести» групп:
(53.48)
где x
l
и x
m
— векторы средних соответственно S
l
и S
m
кластеров;
•
расстояние, измеряемое по принципу «средней связи», определяемое как среднее арифметическое
всех попарных расстояний между представителями рассматриваемых групп:
(53.49)
Академиком А.Н. Колмогоровым было предложено «обобщенное расстояние» между классами,
которое включает в себя в качестве частных случаев все рассмотренные выше виды расстояний.
Расстояния между группами элементов — особенно важный параметр в так называемых
агломеративных иерархических кластер-процедурах, так как принцип работы таких алгоритмов состоит
в последовательном объединении элементов, а затем и целых групп: сначала — самых близких, а
впоследствии — все более и более отдаленных друг от друга. При этом расстояние между кластером S
l
и кластером
S
(m,q)
, являющимся объединением двух других кластеров —
S
m
и
S
q
можно определить по
формуле
(53.50)
где
?
lm
= ? (S
l
, S
m
); ?
lq
= ? (S
l
, S
q
) и
?
mq
= ? (S
m
, S
q
) - расстояния между кластерами S
l
,
S
m
и S
q
;
?, ?, ?
и
?
— числовые коэффициенты, значения которых определяют специфику процедуры, ее
алгоритм.
Например, при
? = ? =
-? = 1/2
и
? = 0
приходим к расстоянию, построенному по принципу
«ближайшего соседа». При
? = ? = ? = 1/2
и
? = 0
расстояние между классами определяется по прин
ципу
«дальнего соседа», т.е. как расстояние между двумя самыми дальними элементами этих классов.
Функционалы качества разбиения

