437
Одно из основополагающих условий метода главных компонент связано с представлением
корреляционной матрицы R через матрицу факторных нагрузок А. Подставив для этого (53.27) в (53.24),
будем иметь
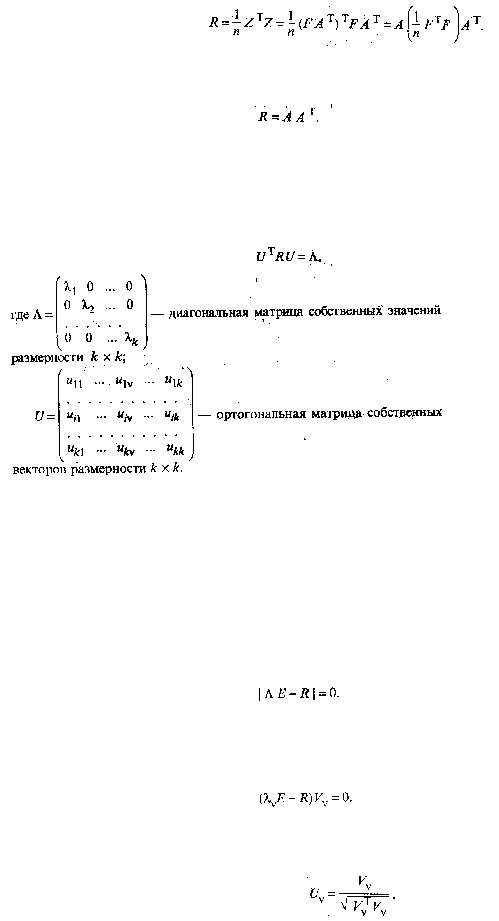
Учитывая (53.28), окончательно получим
(53.33)
Перейдем теперь непосредственно к отысканию собственных значений и собственных векторов
корреляционной матрицы R.
Из линейной алгебры известно, что для любой симметричной матрицы R всегда существует такая
ортогональная матрица U, что выполняется условие
(53.34)
Так как матрица R положительно определена, т.е. ее главные миноры положительны, то все
собственные значения
?
v
> 0 для любых v =1, 2, ..., k.
В компонентном анализе элементы матрицы
?
ранжированы:
?1
?
?
2
? ... ? ?
v
...
?
?
k
? 0. Как будет
показано ниже, собственное значение
?
v
характеризует вклад v-й главной компоненты в суммарную
дисперсию исходного признакового пространства.
Таким образом, первая главная компонента вносит наибольший вклад в суммарную дисперсию, а
последняя, k-я, — наименьший.
В ортогональной матрице U собственных векторов v-й столбец является собственным вектором,
соответствующим
?
v
-му значению.
Собственные значения
?
1
?
...
?
?
v
.... ? ?
k
находятся как корни характеристического уравнения
(53.35)
Собственный вектор V
v
, соответствующий собственному значению
?
v
корреляционной матрицы R,
определяется как отличное от нуля решение уравнения, которое следует из (53.34):
(53.36)
Нормированный собственный вектор U
v
равен

