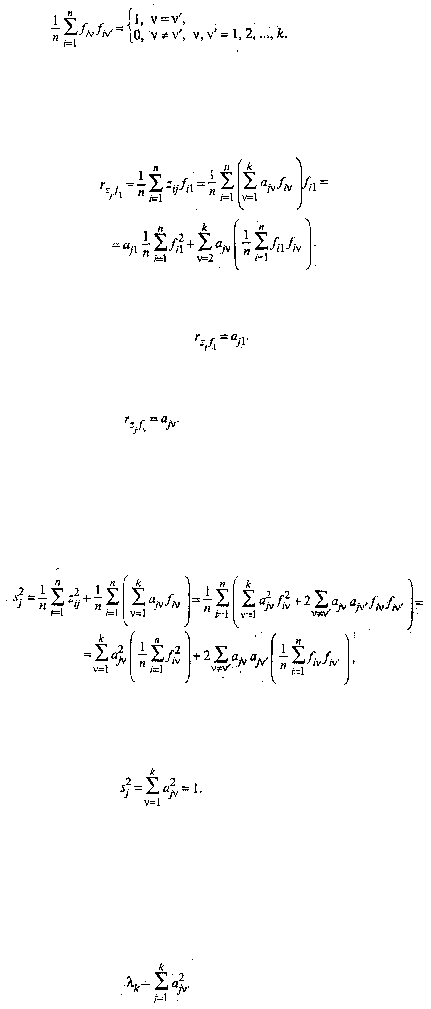
436
(53.29)
С целью интерпретации элементов матрицы А рассмотрим выражение для парного коэффициента
корреляции между переменной z
j
и, например, f1-й главной компонентой. Так как z
о
и f1 нормированы,
будем иметь с учетом (53.26):
Принимая во внимание (53.29), окончательно получим
Рассуждая аналогично, можно записать в общем виде
(53.30)
для всех j = 1, 2, .,., k и v = 1, 2, .... k.
Таким образом, элемент a
jv
матрицы факторных нагрузок А характеризует тесноту линейной связи
между исходной переменной z
j
и главной компонентой f
v
, т.е. –1 ? a
jv
? +1.
Рассмотрим теперь выражение для дисперсии нормированной переменной z
j
. С учетом (53.26) будем
иметь
где v, v'= 1, 2, ..., k.
Учитывая (53.29), окончательно получим
(53.31)
По условию, переменные z
j
нормированы и
s
2
о
= 1. Таким образом, дисперсия переменной z
j
,
согласно (53.31), представлена своими составляющими, определяющими долю вклада в нее всех k
главных компонент.
Полный вклад v-й главной компоненты в дисперсию всех k исходных признаков вычисляется по
формуле
(53.32)

