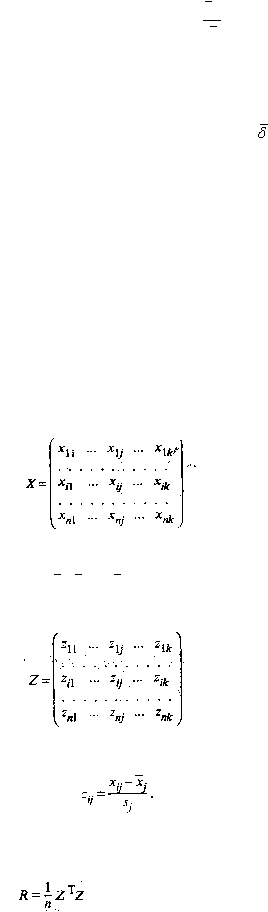
434
Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни приводит к
росту урожайности зерновых в среднем на 0,345 ц/га (b1 = 0,345).
Коэффициенты эластичности Э1 = 0,068 и Э
4
= 0,161 (Э
j
=
y
x
b
j
j
) показывают,
что при увеличении
показателей x1 и х
4
на 1% урожайность зерновых повышается соответственно на 0,068% и 0,161%.
Множественный коэффициент детерминации r
2
y
= 0,469 свидетельствует о
том, что только 46,9% вариации
урожайности объясняется вошедними в модель показателями (x1 и x
4
), т.е. насыщенностью растениеводства
тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (х2, x3, х
5
,
погодными условиями и др.). Средняя относительная ошибка аппроксимации
= 10,5% свидетельствует об
адекватности модели, так же как и величина остаточной дисперсии s² = 1,97.
53.3. Компонентный анализ
Компонентный анализ предназначен для преобразования системы k исходных признаков в систему k
новых показателей (главных компонент). Главные компоненты не коррелированы между собой и
упорядочены по величине их дисперсий, причем первая главная компонента имеет наибольшую
дисперсию, а последняя, k-я
— наименьшую. При этом выявляются неявные, непосредственно не
измеряемые, но объективно существующие закономерности, обусловленные действием как внутренних,
так и внешних причин.
Компонентный анализ является одним из основных методов факторного анализа. В задачах
снижения размерности и классификации обычно используются т первых компонент (т << k).
При наличии результативного признака у может быть построено уравнение регрессии на главных
компонентах.
На основании матрицы исходных данных
размерности п х k, где х
ij
.— значение j-го показателя у i-го наблюдения (i = 1, 2, ..., n; j = 1, 2, .... k),
вычисляют средние значения показателей
k
x
x2
x
,...,
,
1
а также
s1, ..., s
k
и матрицу нормированных
значений
с элементами
Рассчитывается матрица парных коэффициентов корреляции:
(53.24)
с элементами

