433
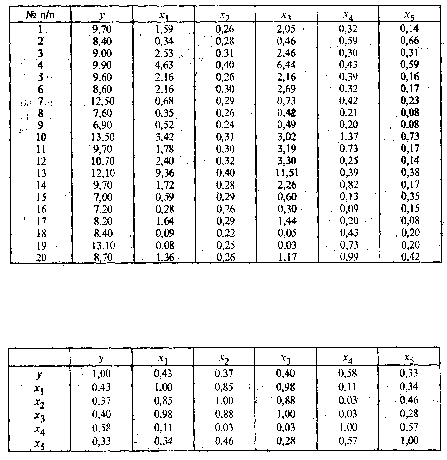
Решение. С целью предварительного анализа взаимосвязи показателей построена матрица ® — таблица
парных коэффициентов корреляции.
Анализ матрицы парных коэффициентов корреляции показывает, что результативный признак наиболее тесно
связан с показателем х
4
— количеством удобрений, расходуемых на гектар (r
yx4
= 0,58).
В то же время связь между аргументами достаточно тесная. Так, существует практически функциональная
связь между числом колесных тракторов (x1) и числом орудий поверхностной обработки почвы x3(r
x1x3
) = 0,98.
О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции r
x1x2
= 0,85 и r
x3x2
= 0,88.
Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим рассчитанное на ЭВМ
регрессионное уравнение урожайности, включив в него все исходные показатели:
yˆ
= 3,515 – 0,006x1 + 15,542x2 + 110x3 + 4,475х
4
- 2,932x
5.
(53.22)
(-0,01) (0,72) (0,13) (2,90) (-0,95)
В скобках указаны t
набл
(?
j
) =
t
j
— расчетные значения t-критерия для проверки гипотезы о значимости
коэффициента регрессии Н
0
: ?
j
= 0, j = 1, 2, 3, 4, 5. Критическое значение
t
кр
= 1,76 найдено по таблице t-
распределения при уровне значимости
?
= 0,1 и числе
степеней свободы
v
= 14.
Из уравнения следует, что
статистически значимым является коэффициент регрессии только при х
4
, так как |t
4
| = 2,90 > t
кр
= 1,76. Не
поддаются экономической интерпретации отрицательные значения коэффициентов регрессии при х1 и x
5
, из чего
следует, что повышение насыщенности сельского хозяйства колесными тракторами (х1) и средствами
оздоровления растений (x
5
) отрицательно сказывается на урожайности. Таким образом, полученное уравнение
регрессии неприемлемо.
После реализации алгоритма пошагового регрессионного анализа с исключением переменных и учетом того,
что в уравнение должна войти только одна из трех тесно связанных переменных (x1,
х2 или x3), получаем
окончательное уравнение регрессии
yˆ
= 7,342 + 0,345x1 + 3,294x
4
. (53.23)
(11,12) (2,09) (3,02)
Уравнение значимо при
? = 0,05,
так как
F
набл
= 266 > F
кр
= 3,20, найденного по таблице F-распределения при
? = 0,05, v1 = 3 и v2 = 17. Значимы и коэффициенты регрессии
?
1
и
?
4
, так как |t
j
| > t
кр
= 2,11 (при
?
= 0,05, v = 17).
Коэффициент регрессии
?
1
следует признать значимым (
?
1
? 0)
из экономических соображений; при этом
t1 = 2,09
лишь незначительно меньше t
кр
= 2,11. В случае если
?
= 0,1, t
кр
= 1,74 и коэффициент регрессии
?
1
статистически значим.

