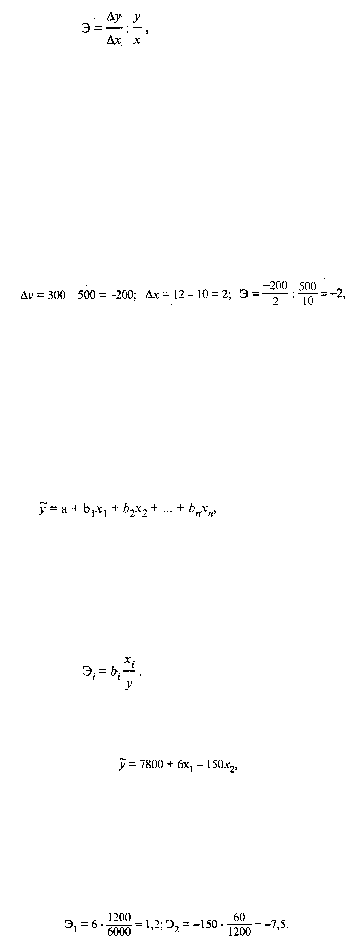
331
цены или дохода, которая выражается в процентном изменении спроса при увеличении факторного
признака (цены, дохода) на один процент. Она измеряется коэффициентом, формула которого:
(38.23)
где Э — коэффициент эластичности;
?
— знак прироста; у
— спрос (косвенно характеризуется
продажей); х — факторный признак: цена или доход.
При Э < 1 наблюдается явление инфраэластичности, товар считается неэластичным и не поддается
регулированию; при Э = 1 спрос считается унитарным, или слабоэластичным, его регулирование не
имеет смысла; при Э > 1 — явление ультраэластичности —
спрос поддается регулированию путем
изменения цен или дохода.
ПРИМЕР. Цена товара Z выросла с 10 руб. за единицу (х
0
)
до 12 руб. (х1). В результате падения спроса
продажа товара сократилась с 500 ед. (у
0
) в предшествовавший изменению цены период до 300 ед. (у1) в период,
последовавший за изменением. Расчет коэффициента эластичности дал следующий результат:
при увеличении цены на 1% спрос сократился на 2%, т.е. он ультраэластичен. Цену можно использовать в
качестве регулятора спроса на товар Z.
У приведенной формулы (ее называют эмпирическим коэффициентом эластичности), несмотря на ее
простоту и доступность, имеется существенный недостаток: она отражает влияние на спрос одного
фактора, при этом подразумевается, что изменение целиком обусловлено действием данного фактора,
хотя на самом деле это не так. На спрос одновременно влияет комплекс факторов, что можно отразить с
помощью многофакторной модели спроса:
(38.24)
где
y
~
— спрос; b
i
— коэффициенты регрессии, отражающие влияние соответствующего i-го фактора; х
i
— факторы; п — число факторов.
По параметрам многофакторного уравнения регрессии можно построить «чистые» коэффициенты
эластичности (их называют «теоретическими»), освобожденные от влияния других факторов
(38.25)
ПРИМЕР. Получена многофакторная линейная модель спроса на товар Q:
где
y
~
— продажа товара Q на душу населения (в шт.);
x1 — доход на душу населения; в среднем равен 1200 руб.;
х2 — цена товара Q; в среднем составляла 60 руб./шт.
Подставляя фактические данные, получаем среднее значение результативного признака:
y
~
= 7800 + 6
• 1200
-
150
• 60 = 6000.

