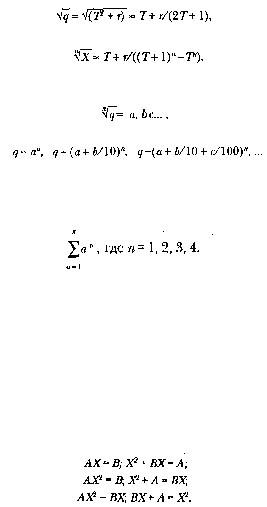
69
Ибн-Рушд разработал также «теорию двух истин» — научно-философской и теологической. Как
наука (философия), так и религия (теология) размышляют прежде всего о Боге — первой и высшей
причине всего существующего и познаваемого. Но они совершенно различны по способу своих
разъяснений. Более совершенный способ дает наука (и философия), опирающаяся на логику и
доказательства. Религия (и теология) дает образное, чувственное познание, представление Бога,
содержащее множество логических противоречий. В Коране можно найти два смысла — буквальный и
«внутренний»: первый постигается богословием, второй — наукой, философией. Теория «двух истин»
способствовала утверждению философских предпосылок естественно-научного познания.
4.2.1. Математические достижения
Арабы существенно расширили античную систему математических знаний. Они заимствовали из
Индии и широко использовали десятичную позиционную систему счисления. Она проникла по
караванным путям на Ближний Восток в эпоху Сасанидов (224—641), когда Персия, Египет и Индия
переживали период культурного взаимодействия. И уже из арифметического трактата аль-Хорезми
«Об индийских числах», переведенного в XII в. на латынь, десятичная система стала известна в
Европе.
Получила также значительное развитие (свойственная еще Древнему Востоку) традиция создания
новых вычислительных приемов и специальных алгоритмов. Так, например, аль-Каши с помощью
вписанных и описанных правильных многоугольников вычислил число
?
до 17 верных знаков.
Развивались методы приближенного извлечения корней. Например, такой известный в древности
прием:
где Т— целое, был распространен на случай любого натурального показателя корня:
Известен им был и метод вычисления корней, который ныне называется методом Руффини —
Горнера*: если
тo последовательное вычисление знаков корня связано с отысканием разностей
* См.: Рыбников К.А. История математики. М., 1974. С. 99.
Арабские математики умели также суммировать арифметические и геометрические прогрессии,
включая нахождение сумм вида:
Не ограничиваясь методами геометрической алгебры, арабские математики смело переходят к
операциям над алгебраическими иррациональностями. Они создали единую концепцию
действительных чисел путем объединения рациональных чисел и отношений и постепенно стерли
грань между рациональными числами и иррациональными. В Европе эту идею восприняли лишь в
XVI в.
Арабские математики совершенствовали методы решения уравнений 2-й и 3-й степеней; решали
отдельные типы уравнений 4-й степени. В трактате аль-Хорезми «Книга об операциях джебр
(восстановление) и кабала (приведение)», по которому европейские ученые в XII в. начали
знакомиться с алгеброй, содержались систематические решения уравнений 1-й и 2-й степени
следующих типов:
Наиболее значительным достижением арабов в алгебре был «Трактат о доказательствах задач»
Омара Хайяма, посвященный в основном кубическим уравнениям. Хайям построил теорию
кубических уравнений, основанную на геометрических методах древних. Он классифицировал все
кубические уравнения с положительными корнями на 14 видов; каждый вид уравнений он решал
соответствующим построением. Хайям пытался найти правило решения кубических уравнений в

