76
кон
Результаты выполнения алгоритма приведены справа. Можно заметить, что результаты вы-
полнения совпадают с описанием выбранного метода решения с помощью дискриминанта. Это
позволяет утверждать, что алгоритм - правильный.
Алгоритм содержит ошибки, если можно указать допустимые исходные данные, при кото-
рых либо будут получены неправильные результаты, либо результаты не будут получены вовсе.
Использование алгоритмов, содержащих ошибки, приводит к созданию программ, также содер-
жащих ошибки.
Алгоритм считается правильным, если он дает правильные результаты для любых допус-
тимых исходных данных. Правильность алгоритмов решения прикладных задач и наличие в них
ошибок можно проверять двумя основными способами.
Первый способ - проверка основных этапов построения алгоритма:
задача
постановка
метод
алгоритм
Второй способ - анализ результатов выполнения алгоритмов и их сравнение с выбранными
методами решения и постановкой задачи:
задача
постановка
метод
алгоритм
Приведем пример построения алгоритма с одновременным анализом его правильности.
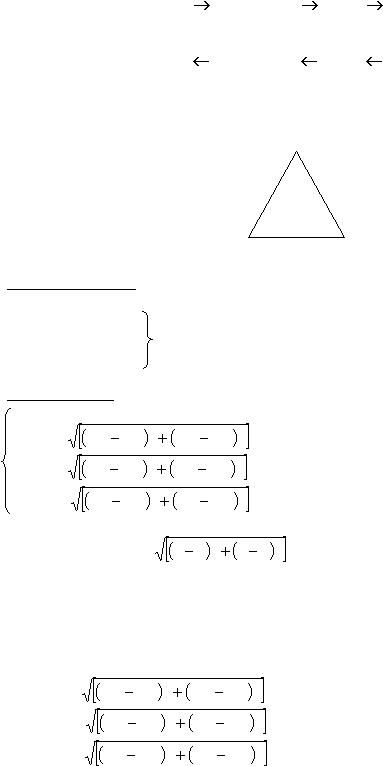
Задача: Определить периметр треугольника, заданного на плоскости координатами вер-
шин.
X
С
,У
С
X
А
,У
А
Xв,Ув
Постановка задачи
Определение периметра треугольника, заданного на плоскости.
Дано: А = (Х
А
, У
А
)
В
=
(Х
В
, У
В
) - координаты вершин треугольника
С = (X
С
,У
С
)
Треб.: Р - периметр
Метод решения
Р = L
АВ
+L
ВС
+L
СА
L
АВ
=
2
В
А
2
B
A
У
У
X
X
L
ВС
=
2
С
В
2
С
В
У
У
X
X
L
СА
=
2
А
С
2
А
С
У
У
X
X
Где: Р = L(A,B) + L(B,C) + L(C,A);
здесь L[(x,y),(u,v)] =
2
2
v
y
u
x
.
Приведем алгоритм, полученный из описания метода упорядочением операций вычисления
длин сторон треугольника с завершающим вычислением периметра. Результаты выполнения алго-
ритма приведены справа.
алг «периметр треугольника»
нач
LAB: =
2
2
В
А
B
A
У
У
X
X
LBC : =
2
2
С
В
С
В
У
У
X
X
LCA : =
2
2
А
С
А
С
У
У
X
X

