218
центру распределения.
Применяется для проверки
нормальности распределения
функции
9. Критерий Фишера
F
Математический критерий,
характеризующий значимость
уравнения регрессии.
Применяется для выбора модели
Больше табличного значения,
установленного для разных
размеров матрицы и вероятностей
10. Критерий
Стьюдента
t
Существенность факторов,
входящих в модель. Применяется
для выбора модели
> 2 (при вероятности 0,95)
11. Среднеквадра-
тическая ошибка
коэффициентов
регрессии
?a
i
Точность полученных
коэффициентов регрессии.
Применяется для оценки
коэффициентов регрессии
В два и более раза меньше
соответствующего коэффициента
регрессии
12. Ошибка
аппроксимации
E
Допуск прогноза или степень
несоответствия эмпирической
зависимости теоретической.
Применяется для оценки
адекватности (точности) модели
|Е| <15%
13. Коэффициент
эластичности
Э
i
Показывает, на сколько процентов
изменяется функция при
изменении соответствующего
фактора на 1 %. Применяется для
ранжирования факторов по их
значимости
>0,01
3.
Построение гистограмм по каждому фактору с целью определения форм распределения
случайных наблюдений.
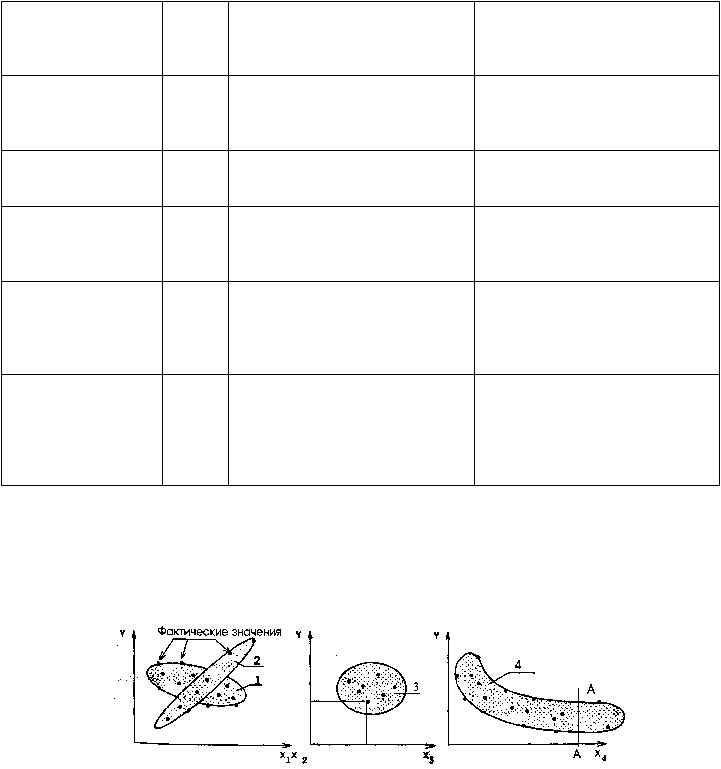
Построение по каждому фактору корреляционных полей, т.е. графическое изображение функций
фактора с целью предварительного определения тесноты и формы связи между функцией и каждым
фактором. Примеры корреляционных полей показаны на рис. 7.2.
Рис. 7.2. Примеры корреляционных полей
Корреляционные поля построены по исходным статистическим данным Х1—Х
4
(факторы) и Y
(функция). Анализ корреляционных полей показывает, что:
а) между Y и Х1 теснота связи слабая, по форме она линейная, обратно пропорциональная;
б) между Y и Х2 теснота связи высокая, по форме она линейная, прямо пропорциональная;
в) между Y и Х3 связи нет, так как функцию Y = f(Х3) можно построить в любом направлении;
г) между Y и Х
4
теснота связи высокая, форма связи — гиперболическая, после линии А—А фактор
Х
4
уже не влияет на Y.
4. Матрица исходных данных составляется по следующей форме:

