104
Дании, Швеции, Германии, Австрии этот показатель колеблется около нулевого значения. В таких
странах, как Италия, Польша, Канада, США, рождаемость пока еще превышает смертность. Однако в
целом в большинстве развитых стран ежегодный прирост населения составляет примерно 0,6% в год,
тогда как в развивающихся странах – 2% в год.
В целом происходит стремительный рост населения на планете, что ставит насущную жизненную
проблему управления природными ресурсами. При этом все отрасли управления ресурсами объединяет
одна наука – экология и одна общая проблема – проблема оптимизации и, наконец, необходимость
использовать одни и те же методы – взятие выборок, статистический анализ, математический анализ,
логические процедуры, связанные с исследованием операций и анализом систем, применение
вычислительной техники. Конечно, анализ и решение такой проблемы и даже какой-либо ее части
представляет собой труднейшую задачу [30].
Начнем с рассмотрения простейшей задачи об оптимальном рационе, математическая модель
которой допускает наглядную геометрическую интерпретацию. Пусть имеется п продуктов питания
(хлеб, мясо, молоко, картофель и т.д.) и т полезных веществ (жиры, белки, углеводы и т.п.). Обозначим
через a
ij
– содержание i-го вещества в единице j-го продукта, через b
i
, – потребность индивидуума в i-м
веществе (скажем, в месяц) и через c
j
, – цену единицы j -го продукта.
Обозначив потребление индивидуумом j-го продукта через х
i
, получаем задачу о выборе наиболее
дешевого рациона питания (стоимости месячной продовольственной потребительской корзины):
min
1
n
j
j
j
x
c
(11.1)
при ограничениях
m
i
b
x
a
j,
j
n
j
ij
,...,
2
,
1
1
(11.2)
и
.
,...,
2
,
1
,
0
n
j
x
j
(11.3)
Такая задача называется задачей линейного программирования (в стандартной форме), общая теория
которой рассмотрена, например, в [2].
Прежде чем исследовать задачу (11.1)–(11.3), заметим, что ее можно представить как задачу
минимизации целевой функции f(x) =
n
j
j
j
x
c
1
.
на множестве точек (x1,...,x
n
), удовлетворяющих
условиям (11.2) и (11.3). Такое множество называется полиэдром и обозначается Р. Итак, мы имеем
экстремальную задачу
f(х)
>
min, х
Р .
(11.4)
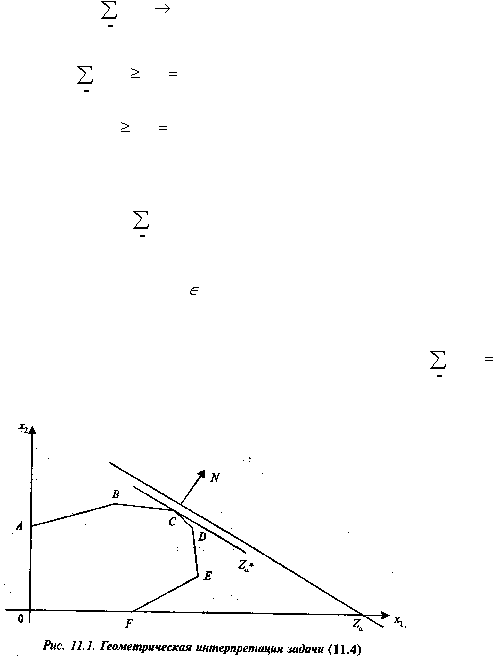
Выясним, что представляет собой данный полиэдр Р на плоскости x1Ox2 в случае двух продуктов x1 и
x2. Из неравенств (11.3) вытекает, что Р расположен в первом квадранте, а каждое неравенство (11.2)
геометрически определяет множество точек, лежащих по одну сторону от прямой
,
2
1
j
j
j
ij
b
x
a
(рис.
11.1), т. е. полиэдр Р представляет собой неограниченное множество в первом квадранте, лежащее вне
области, ограниченной многоугольником OABCDEF.

