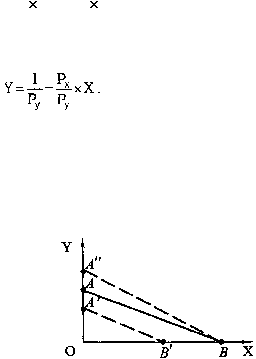
22
1.2.4. БЮДЖЕТНЫЕ ОГРАНИЧЕНИЯ
Как уже отмечалось ранее, каждый рациональный потребитель стремится максимизировать
совокупную полезность, которую он получает за счет своего бюджета.
Если в количественной теории потребитель свои вкусы и предпочтения выражает в виде системы
показателей предельной полезности благ и графиков MU и TU, то в порядковой теории в качестве
средства выражения системы предпочтений потребителя выступает карта безразличия. При этом
потребитель знает, что самые предпочтительные наборы находятся на наиболее удаленной от начала
координат кривой безразличия. Но «дотянуться» до такой кривой безразличия потребитель, как
правило, не может. Этому мешает недостаточность его бюджета.
Все доступные конкретному потребителю товарные наборы могут быть выражены с помощью его
бюджетной линии, если ее поместить в ту же систему координат, в которой находятся кривые
безразличия.
Для построения бюджетной линии необходимо иметь уравнение этой линии. Его обоснование
происходит следующим образом.
Пусть месячный доход потребителя составляет I (руб.). Предположим далее, что потребитель весь
свой доход тратит на приобретение только двух товаров Х и Y.
Его бюджетное ограничение в этом случае может быть представлено в виде следующего равенства:
I = P
x
X + P
y
Y.
(1.18)
Смысл бюджетного ограничения, как видим, сводится к тому, что расходы потребителя на
приобретение товаров Х и Y не могут превышать его дохода. Уравнение бюджетной линии выводится
непосредственно из равенства (1.14). Оно имеет следующий вид:
(1.19)
На рис. 1.10 бюджетная линия изображена в виде отрезка АВ. Поскольку бюджетная линия всегда
представляет собой прямую, пересекающую оси координат, то для ее построения может быть применен
более простой метод. Достаточно найти лишь точки пересечения бюджетной линии с осями координат
(то есть точки А и В) и соединить их прямой линией. Полученная прямая и является как раз бюджетной
линией.
Рис. 1.10. Бюджетная линия
Положение точки А определяется длиной отрезков ОА, а положение точки В – длиной отрезка OВ.
Каждый из этих отрезков соответствует количеству единиц товара Y или товара X, которое может
приобрести потребитель, потратив весь свой доход только на этот товар. В связи с этим длина отрезка
ОА соответствует I / P
y
, а длина отрезка OB – 1/Р
x
. В свою очередь, наклон бюджетной линии равен
коэффициенту при Х в уравнении (1.19), то есть Р
х
/ Р
у
.
Все наборы из товаров Х и Y, расположенные на бюджетной линии, по своей стоимости четко
соответствуют доходу потребителя I, а значит, являются доступными для него. К числу доступных
относятся также все товарные наборы, расположенные ниже бюджетной линии. Стоимость каждого из
них ниже I. Зато все наборы, находящиеся выше бюджетной линии, стоят больше I и потому являются
недоступными для данного потребителя.
1.2.4.1. Изменения в доходе и ценах
Анализируя уравнение бюджетной линии (1.19), можно сделать вывод, что ее положение зависит как
от дохода потребителя, так и от цен товаров. Если бы доход потребителя оказался меньше, а цены
прежними, то в этом случае бюджетная линия сместилась бы вниз (А'В'). При этом она была бы
параллельна линии АВ, так как коэффициент Р
x
/ Р
y
остался бы прежним. Если бы доход потребителя и

