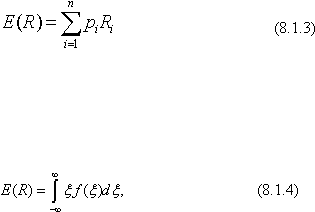
305
Для инвестора акция не просто предмет купли-продажи, но и владение частью реального актива,
поток будущих дивидендов, возможность доступа к управлению корпорацией.
Источники риска, связанные с вложениями в ценные бумаги, разнообразны. При этом речь идет
только о риске того, что мы получим не такую доходность, какую ожидали. Если быть более точным, то
риск связан с тем, что мы получим доходность меньше, чем ожидали, или убыток. Формула (8.1.1)
сразу указывает на ряд причин риска, типичных для обыкновенных акций: неизвестна величина диви-
дендов
D. (она зависит от общей продуктивности фирмы, от решений по вложениям в расширение
производства и т. п.), неизвестна цена Р1, в конце года, зависящая от репутации и политики компании,
общей конъюнктуры на фондовом рынке, политической обстановки (например, цена может сильно
измениться в условиях грядущей национализации корпорации). Сказанное позволяет интерпретировать
доходность как случайную величину, принимающую конкретные значения в многообразных состояниях
реального мира.
В случае привилегированной акции нет (или почти нет) неопределенности по дивидендам, но цена Р1
по-прежнему неизвестна.
Обладатели облигаций корпорации должны получить заранее оговоренные платежи, поэтому здесь
нет неопределенности по D1 и Р1. Однако во всех случаях есть опасность, что дела корпорации пойдут
плохо и она станет неплатежеспособной или обанкротится.
26
26
S. Lumby. Investment Appraisal and Financial Decisions. First Course in Financial Management. Wokingham: VNR, 1988.
Перейдем к формальным определениям доходности и риска. Заранее заметим, что если определение
доходности не вызывает особых споров и хорошо понятно интуитивно, то с определением риска дело
обстоит значительно сложнее.
Пусть R — доходность финансового актива. Выше уже было сказано, что R является случайной
величиной. Ожидаемой доходностью называется величина E(R) — математическое ожидание случайной
величины R. Это определение соответствует стандартной интерпретации математического ожидания
как среднего значения величины с учетом распределения ее вероятностей.
Если считать, что мир может находиться в конечном числе состояний, то случайная величина R
дискретна. Если ее закон распределения задается равенствами
P(R = R
i
) = p
i
(i = 1,2,...,n), где R
i
— всевозможные значения, которые принимает R, то
Однако реальное количество существенно различных состояний мира столь велико, что естественно
считать распределение вероятностей R непрерывным (хотя на самом деле цена ценной бумаги не
принимает произвольные вещественные значения — есть минимальная нормативная величина
изменения цены). Поэтому
где f(?) — плотность распределения вероятностей случайной величины R. Теория портфеля Г.
Марковица предполагает, что доходности ценных бумаг следуют нормальному закону, который
является одним из наиболее изученных.
27
27
D. R. Harrington. Modern Portfolio Theory and Capital Asset Pricing Model. A User's Guide. N. Y.: Prentice-Hall, 1983.
H. Markowitz. Mean-Variance Analysis in Portfolio Choice and Capital Financial. Oxford, 1987.
H. Markowitz. Portfolio selection. —Journal of Finance, 1952, ¹ 3. H. Markowitz. Portfolio selection: Efficient Diversification of
Investments. Oxford: Blackwell, 1991.

