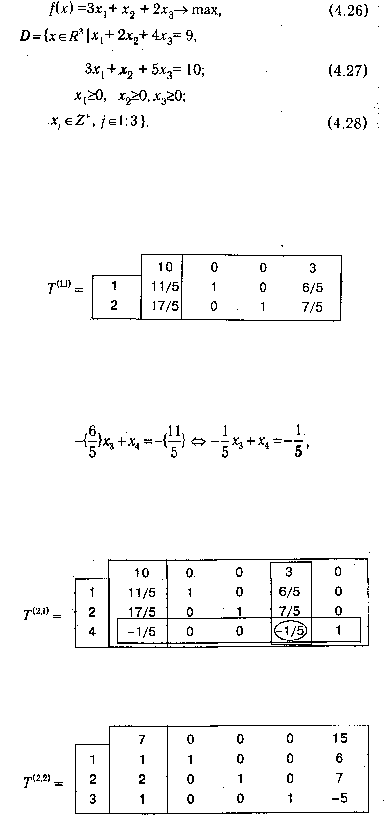
82
целочисленного плана.
4.2.3. Пример решения ЦЗЛП методом Гомори. Рассмотрим особенности применения метода
Гомори на конкретном примере. Пусть дана задача со следующими условиями:
Итерация 1. Используя обычный симплекс-алгоритм, решаем непрерывный аналог исходной задачи,
в котором игнорируются условия целочисленности (4.28). В качестве исходного базиса можно взять
первый и второй столбцы. На его основе заполняется таблица T
(1,1)
(первый индекс в обозначении
таблицы соответствует «большой» итерации, а второй — «малой»).
Как видно из строки оценок, данный базис является оптимальным, однако соответствующий ему
план х
={11/5,17/5, 0)
не является целочисленным, поэтому выбираем из таблицы T
(1,1)
строку,
содержащую первый нецелый элемент, и согласно формуле (4.25) строим отсекающее ограничение:
после чего переходим к следующей «большой» итерации.
Итерация 2. С учетом сформированного отсекающего ограничения заполняем симплекс-таблицу
T
(2,1)
.
В соответствии с алгоритмом двойственного симплекс-метода переходим к следующему базису
N(?
(2,2)
)={1, 2, 3}.
План, достигнутый в таблице
T
(2,2)
, является не только оптимальным (b(?
(2,2)
)>0), но и полностью
состоит из целочисленных компонент, т. е. решение задачи найдено: х* = (1, 2, 1) и f(x)=7.
4.3. МЕТОД ВЕТВЕЙ И ГРАНИЦ
4.3.1. Общая схема метода «ветвей и границ». Другим широко применяемым для решения задач

