62
величину:
Очевидно, что на каждом шаге выполняется хотя бы одно из равенств: а
i
(q+1)
= 0 или b
j
(q+1)
= 0 . Если
справедливо первое, то это означает, что весь запас i-го пункта производства исчерпан и необходимо
перейти к распределению запаса в пункте производства i +1, т. е. переместиться к следующей клетке
вниз по столбцу. Если же b
j
(q+1)
= 0, то значит, полностью удовлетворена потребность для j-го пункта,
после чего следует переход на клетку, расположенную справа по строке. Вновь выбранная клетка
становится текущей, и для нее повторяются все перечисленные операции.
Основываясь на условии баланса запасов и потребностей (3.5), нетрудно доказать, что за конечное
число шагов мы получим допустимый план. В силу того же условия число шагов алгоритма не может
быть больше, чем m+n-1, поэтому всегда останутся свободными (нулевыми) mn-(m+n-1) клеток.
Следовательно, полученный план является базисным. Не исключено, что на некотором промежуточном
шаге текущий нераспределенный запас оказывается равным текущей неудовлетворенной потребности
(а
i
(q)
= b
j
(q)
). В этом случае переход к следующей клетке происходит в диагональном направлении
(одновременно меняются текущие пункты производства и потребления), а это означает «потерю» одной
ненулевой компоненты в плане или, другими словами, вырожденность построенного плана.
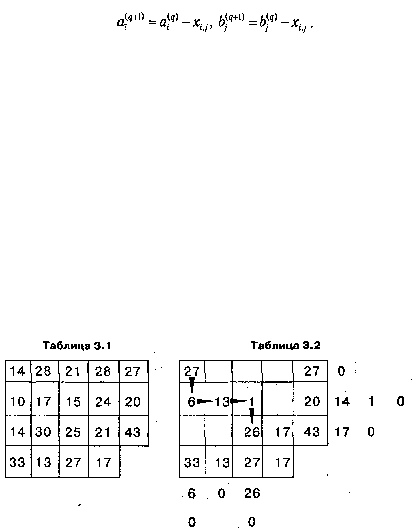
Рассмотрим применение метода северо-западного угла на конкретном примере. Транспортная
таблица 3.1 содержит условия некоторой задачи, а в табл. 3.2 показан процесс поиска допустимого
плана, включая последовательное изменение объема нераспределенных запасов и неудовлетворенных
потребностей. Стрелки отражают траекторию перехода по клеткам транспортной таблицы, а цифры,
находящиеся за ее пределами, — текущие нераспределенные остатки после назначения объема для
очередной клетки.
Особенностью допустимого плана,, построенного методом северо-западного угла, является то, что
целевая функция на нем принимает значение, как правило, далекое от оптимального. Это происходит
потому, что при его построении никак не учитываются значения с
i,j
. В связи с этим на практике для по-
лучения исходного плана используется другой способ — метод минимального элемента, в котором при
распределении объемов перевозок в первую очередь занимаются клетки с наименьшими ценами.
3.1.3. Критерий оптимальности. Рассмотрим более подробно структуру матрицы транспортной
задачи. Схематично она показана на рис. 3.2.
Из него видно, что матрица имеет размерность (m+n) х mn, состоит из нулей и единиц и распадается
на две группы однотипных блоков. Первая (верхняя) соответствует ограничениям на

