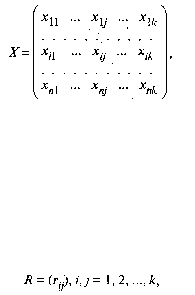
442
Решение другой задачи заключается в определении естественного расслоения результатов
наблюдений на четко выраженные кластеры, лежащие друг от друга на некотором расстоянии.
Если первая задача типизации всегда имеет решение, то во втором случае может оказаться, что
множество наблюдений не обнаруживает естественного расслоения на кластеры, т.е. образует один
кластер.
Хотя многие методы кластерного анализа довольно элементарны, основная часть работ, в которых
они были предложены, относится к
последнему десятилетию. Это объясняется тем, что эффективное
решение задач поиска кластеров, требующее выполнения большого числа арифметических и
логических операций, стало возможным только с возникновением и развитием вычислительной
техники.
Обычной формой представления исходных данных в задачах кластерного анализа служит матрица
каждая строка которой представляет результаты измерений k рассматриваемых признаков у одного из
обследованных объектов. В конкретных ситуациях может представлять интерес как группировка
объектов, так и группировка признаков. В тех случаях, когда разница между двумя этими задачами не
существенна, например при описании некоторых алгоритмов, мы будем пользоваться только термином
«объект», включая в это понятие и термин «признак».
Матрица Х не является единственным способом представления данных в задачах кластерного
анализа. Иногда исходная информация задана в виде квадратной матрицы
элемент r
ij
которой определяет степень близости i-го объекта к j-му.
Большинство алгоритмов кластерного анализа полностью исходит из матрицы расстояний (или
близостей) либо требует вычисления отдельных ее элементов, поэтому если данные представлены в
форме X, то первым этапом решения задачи поиска кластеров будет выбор способа вычисления
расстояний, или близости, между объектами или признаками.
Несколько проще решается вопрос об определении близости между признаками. Как правило,
кластерный анализ признаков преследует те же цели, что и факторный анализ: выделение групп
связанных между собой признаков, отражающих определенную сторону изучаемых объектов. Мерой
близости в этом случае служат различные статистические коэффициенты связи.
Расстояние между объектами (кластерами) и мера близости
Наиболее трудным и наименее формализованным в задаче классификации является определение
понятия однородности объектов.
В общем случае понятие однородности объектов задается введением либо правила вычисления
расстояний
?(
x
i
, х
j
) между любой парой исследуемых объектов (x1, x2, ...,x
n
), либо некоторой функцией
r(х
i
,
x
j
), характеризующей степень близости i-го и j-го объектов.
Если задана функция
?(
x
i
, х
j
), то близкие с точки зрения этой метрики объекты считаются
однородными, принадлежащими к одному классу. Очевидно, что необходимо при этом сопоставлять
?(x
i
, х
j
) с некоторыми пороговыми значениями, определяемыми в каждом конкретном случае по-своему.
Аналогично используется и мера близости r(x
i
, х
j
), при задании которой мы должны помнить о
необходимости выполнения следующих условий: симметрии r(x
i
, х
j
) = r(x
j
, х
i
); максимального сходства
объекта
с самим собой r(x
i
, х
i
) =
ij
max
r(x
i
, х
j
), 1 ? i, j
?
п, и монотонного убывания
r(x
i
, х
j
) по мере
увеличения ?(x
i
, х
j
), т.е. из ?(x
k
, х
l
)
?
?(x
i
, х
j
) должно следовать неравенство r(x
k
, х
l
)
?
?(x
i
, х
j
).
Выбор метрики, или меры близости, является узловым моментом исследования, от которого в

