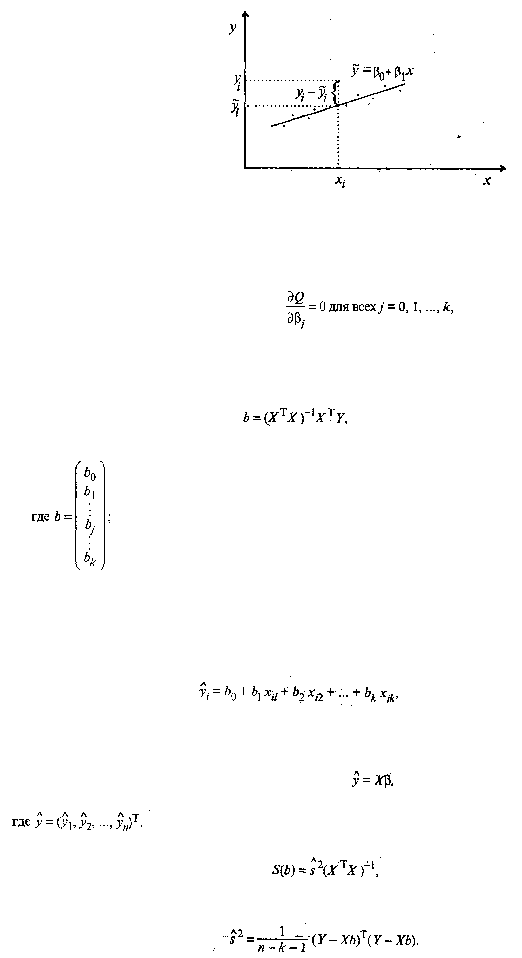
430
Рис. 53.1. Наблюдаемые и модельные значения результативного признака у
Дифференцируя, с учетом (53.11) и (53.10), квадратичную форму
Q по ?
0
, ?1, …, ?
k
и приравнивая
частные производные к нулю, получим систему нормальных уравнений
решая которую получим вектор-столбец оценок b, где b = (b
0
, b1, ..., b
k
)
T
. Согласно методу наименьших
квадратов, вектор-столбец оценок коэффициентов регрессии получается по формуле
(53.12)
Х
T
— транспонированная матрица X;
(Х
T
Х)
-1
— матрица, обратная матрице Х
T
Х.
Зная вектор-столбец b оценок коэффициентов регрессии, найдем оценку
i
y
ˆ
уравнения регрессии
(53.13)
или в матричном виде:
Оценка ковариационной матрицы вектора коэффициентов регрессии b определяется выражением
(53.14)
где
(53.15)
Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов
регрессии, имеем

