63
Принципы логического вывода в Прологе в отличие от традиционной формальной логики
основаны на использовании предикатов. Выражение этого закона Аристотеля на языке предикатов дает
конструктивную процедуру вывода конкрентых следствий из общих правил и конкретных фактов.
Закон противоречия в записи на языке исчисления предикатов преобразуется в процедуру вывода
ответов на простейшие вопросы вида ? А(с):
Содержательный смысл: при противоречии А(х) и не А(с) контрпримером служит х = с. Здесь х —
переменная, а с
— конкретное значение, при котором отрицание ответа оказывается ложным. Это
значение х = с выводится системой Пролог в качестве ответа. Примеры:
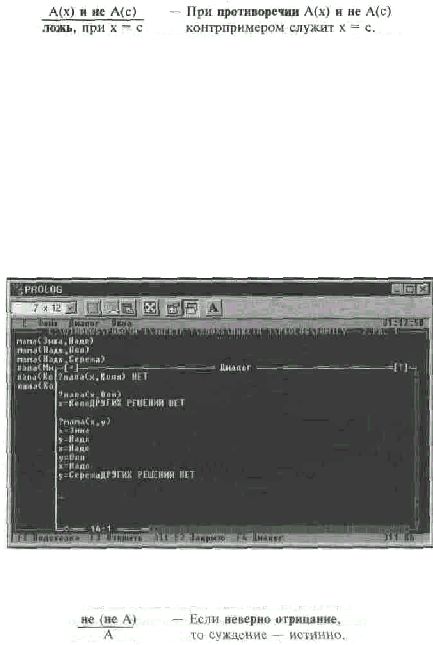
? папа(х,Коля) нет
—
Кто папа у Коли?
? папа(х,Оля)
—
Кто папа у Оли?
х = Коля
? мама(х,у)
—
Что известно о мамах?
х = Зина у = Надя
х = Надя у = Оля
Закон двойного отрицания — третий общий закон формальной логики, указанный Аристотелем:
Примеры рассуждений:
1. Неверно, что «вчера не было дождя».
Следовательно, «вчера был дождь».
2. Неправда, что «это сделал не Саша».
Следовательно, «это сделал Саша». (?)
Из второго примера видно, что закон двойного отрицания является косвенным доказательством,
поскольку оно не опирается на факты или аргументы. По этим причинам закон двойного отрицания
может оказаться ошибочным и этот закон не является общезначимым (верным для всех случаев и
ситуаций).
Правильность утверждений и рассуждений даже при безупречной логике доказательств зависит от
достоверности исходных фактов и положений. Эту идею выражает четвертый общий логический закон

