55
В(х, у) = « х < у»,
где х, у — это некоторые переменные (объекты).
Значениями переменных в предикатах могут быть числа, слова, векторы, списки, функции,
процедуры, алгоритмы, программы, более точно — конструктивные объекты. Для математической
логики существенно, чтобы эти объекты имели конструктивную форму и были бы строго определены.
Примеры обозначения предикатов с конкретными значениями:
А (красный) = «цвет = красный»;
В (рост, 180) = «рост < 180»;
В (рост, у) = «рост < у».
Из приведенных примеров предикатов и высказываний понятно, что семантика языков запросов в
Интернет описывается законами исчисления высказываний, а семантика языков запросов к базам
данных на ЭВМ — законами исчисления предикатов (с равенствами).
Истинность сложных высказываний и предикатов может исследоваться через анализ их
всевозможных интерпретаций либо путем их доказательства или опровержения. Так для опровержения
любого общего утверждения достаточно указать хотя бы один контрпример.
Исчерпывающий анализ сложных высказываний проводится с помощью таблиц истинности,
рассмотренных в предыдущем разделе. Высказывание — общезначимо (тождественно истинно), если
оно истинно при любых значениях входящих в него суждений.
Доказательство
— это последовательность суждений, обосновывающих некоторое утверждение.
Собственно доказательства строятся на основе некоторых правил вывода, в которых одни утверждения
являются (пред)посылками, а другие — их следствиями.
На практике исходным для доказательства утверждений являются некоторые факты и аргументы. В
математике доказательства опираются на аксиомы, принятые в рассматриваемой теории, истинность
которых не обсуждается.
Важнейшей операцией математической логики, на которой построены основные математические
исследования теорий и доказательства теорем, является импликация, имеющая обозначение А > В.
Импликация А
>
В
— это логическое следование. Импликация А > В читается: «если А, то В»,
«из А следует В», «А влечет В» и т. п. Первое суждение в импликации называется посылкой, а второе
— следствием.
Примеры правил логического вывода:
а) над высказываниями:
если «на улице дождь», то «на улице мокро»;
б) над предикатами:
любит (х, конфеты)
>
сластена (х).
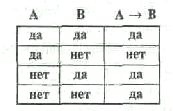
Таблица истинности импликации:
Свойства импликации:
П1:
«Импликация А
>
В
ложна,
когда посылка А истинна, а следствие В — ложно».
П2:
«Импликация А
>
В
истинна,
когда истинно следствие либо ложны и посылка и следствие».
Общий закон логического вывода был указан Аристотелем — основателем логики как научной
дисциплины — и назван modus ponens:

