110
Исчерпывающий анализ правильности алгоритмов и устранение из программ ошибок всех
перечисленных типов возможны только при наличии соответствующих спецификаций: постановок
задач, описаний методов решения и спецификаций ввода-вывода данных.
Будем считать, что программа правильная, если она дает правильные результаты для любых
допустимых исходных данных. Такого рода программы вполне можно использовать для решения
прикладных задач.
Программа считается надежной, если она не дает сбоев и отказов ни при каких исходных данных.
Надежность - обязательное условие для всех программ, которые используются людьми для решения
практических задач на ЭВМ.
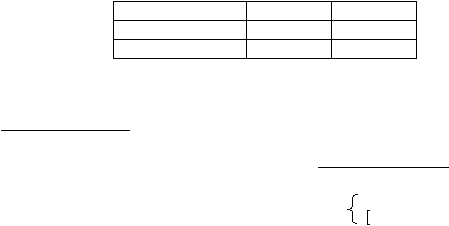
В качестве иллюстрации приведем пример систематического составления алгоритма и программы
задачи определения суммарного веса учеников по данным из таблицы:
фамилия
рост
вес
Иванов
185
85
Петрова
165
65
Сидоров
170
80
Рассмотрим постановку задачи и метод вычисления суммарного веса.
Постановка задачи
Определение суммарного веса.
Дано:
Метод вычисления
(D1,.., D
N
)
- данные об учениках,
S
0
= 0
где D = [Fam,R,V] - состав данных,
S
k
= S
k-1
+ v
k
Fam - фамилия, R - рост, V - вес.
k = (1 ... N)]
Треб.: V
sum
- суммарный вес.
V
sum
= S
N
Где: V
sum
= v1 + v2 + ... + v
N
При: N > 0.
Правильность метода вычислений можно доказать по индукции. Рассмотрим результаты вычислений
на 1-м, 2-м и k-м шагах. Отметим, что начальное значение S
0
= 0.
На первом шаге при k = 1 результат вычисления
S1 = S
0
+v1 = v1 .
На следующем, втором шаге при k = 2 результат
S2 = S1 + v2 = v1 + v2.
На третьем шаге при k = 3 результат
S3= S2 + v3 = v1 + v2 + v3.
В общем случае можно предположить, что к k-му шагу результат вычисления
S
k-1
=v1+...+v
k-1
.
Тогда результат вычислений после k-го шага (исходя из описания метода)
S
k
= S
k-1
+v
k
= v1 + … + v
k-1
+ v
k
.
В силу принципа математической индукции утверждение верно для всех k = 1, 2,.... N.
Следовательно, на последнем шаге при k = N конечный результат:
S
N
= v1 + ... + v
N
.

